Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-26T00:58:35.341Z Has data issue: false hasContentIssue false
  • English
  • Français

Fourier multipliers on spaces of distributions

Published online by Cambridge University Press:  20 January 2009

W. Lamb
W. Lamb
Affiliation:
Department of Mathematics, University of Strathclyde, Glasgow
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In [8], Rooney defines a class 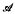of complex-valued functions ζ each of which is analytic in a vertical strip α(ζ)< Res < β(ζ) in the complex s-plane and satisfies certain growth conditions as |Im s| →∞ along fixed lines Re s = c lying within this strip. These conditions mean that the functions

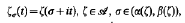
fulfil the requirements of the one-dimensional Mihlin-Hörmander theorem (see [6, p. 417]) and so can be regarded as Fourier multipliers for the Banach spaces 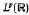. Consequently, each function 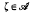gives rise to a family of bounded operators W[ζ,σ] σ ∈(α(ζ),β(ζ)), on 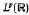, 1<p<∞.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 29 , Issue 3 , October 1986 , pp. 309 - 327
Copyright
Copyright © Edinburgh Mathematical Society 1986

References

REFERENCES

1.Copson, E. T., Partial differential equations (Cambridge University Press, 1975).CrossRefGoogle Scholar
2.Erdelyi, A., et al. , Tables of integral transforms {Vol. 1) (McGraw-Hill, New York, 1954).Google Scholar
3.Lamb, W., A distributional theory of fractional calculus, Proc. Royal Soc. Edinburgh 99A (1985), 347–357.CrossRefGoogle Scholar
4.Lebedev, N. N., Special functions and their applications (Dover, New York, 1972).Google Scholar
5.Mcbride, A. C., Fractional calculus and integral transforms of generalized functions (Research Notes in Mathematics 31, Pitman, London, 1979).Google Scholar
6.Okikiolu, G. O., Aspects of the theory of bounded integral operators in Lp-spaces (Academic Press, London, 1971).Google Scholar
7.Rooney, P. G., On the ranges of certain fractional integrals, Canad. J. Math. 24 (1972), 1198–1216.CrossRefGoogle Scholar
8.Rooney, P. G., A technique for studying the boundedness and extendability of certain types of operators, Canad. J. Math. 25 (1973), 1090–1102.CrossRefGoogle Scholar
9.Schwartz, L., Theorie des distributions (Hermann, Paris, 1966).Google Scholar
10.Zemanian, A. H., Distribution theory and transform analysis (McGraw-Hill, New York, 1965).Google Scholar
11.Zemanian, A. H., Generalized integral transformations (Interscience, New York, 1968).Google Scholar