Hostname: page-component-745bb68f8f-v2bm5 Total loading time: 0 Render date: 2025-01-11T17:31:38.084Z Has data issue: false hasContentIssue false
  • English
  • Français

Failing Cases of Fourier's Double-Integral Theorem

Published online by Cambridge University Press:  20 January 2009

Peter Alexander
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Fourier's Theorem, as usually stated, is

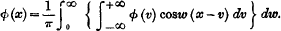
Most writers give this without limitation, but De Morgan (Diff. and Int. Calc. pp. 618 &c.) directs attention to what he calls the apparent neglect by previous writers of the limitation of the theorem to functions which satisfy the condition

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 3 , February 1884 , pp. 12 - 18
Copyright
Copyright © Edinburgh Mathematical Society 1884

References

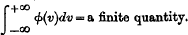
* G(regory ?). On Fourier&s Theorem. Cambridge Mathematical Journal, HI., pp. 288–290.

Walton, W. A demonstration of Fourier&s Theorem. Quarterly Journal of Mathematics, VIII., pp. 136–138.Google Scholar

Glaither, J. W. L. On Fourier&s double-integral Theorem. Messenger of Mathematics, II., pp. 20–24. Google Scholar

Du Bois Beymond, P. Sur les formules de représentation dee fonctioiis Comptes rendus… Paris, XCH., pp. 915–918, 962–964.Google Scholar

These are in addition to the list given by Freeman at the place above cited.