Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Aitken, A. C.
1953.
A Note on Trace-Differentiation and the Ω-operator.
Proceedings of the Edinburgh Mathematical Society,
Vol. 10,
Issue. 1,
p.
1.
Wallace, Andrew H.
1953.
A Note on the Capelli Operators associated with a Symmetric Matrix.
Proceedings of the Edinburgh Mathematical Society,
Vol. 9,
Issue. 1,
p.
7.
Shimura, Goro
1984.
On differential operators attached to certain representations of classical groups.
Inventiones Mathematicae,
Vol. 77,
Issue. 3,
p.
463.
Howe, Roger
and
Umeda, T�ru
1991.
The Capelli identity, the double commutant theorem, and multiplicity-free actions.
Mathematische Annalen,
Vol. 290,
Issue. 1,
p.
565.
Ørsted, Bent
and
Zhang, Genkai
1995.
Generalized principal series representations and tube domains.
Duke Mathematical Journal,
Vol. 78,
Issue. 2,
Caracciolo, Sergio
Sokal, Alan D.
and
Sportiello, Andrea
2013.
Algebraic/combinatorial proofs of Cayley-type identities for derivatives of determinants and pfaffians.
Advances in Applied Mathematics,
Vol. 50,
Issue. 4,
p.
474.
Faifman, Dmitry
2017.
Crofton formulas and indefinite signature.
Geometric and Functional Analysis,
Vol. 27,
Issue. 3,
p.
489.
Bernig, Andreas
Faifman, Dmitry
and
Solanes, Gil
2022.
Crofton formulas in pseudo-Riemannian space forms.
Compositio Mathematica,
Vol. 158,
Issue. 10,
p.
1935.
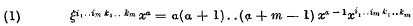
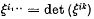 with i = i1,..im; k= k1,…km and xi,… is the algebracial complement of
with i = i1,..im; k= k1,…km and xi,… is the algebracial complement of 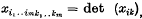 i = i1,..im; k = k1,…km, in
i = i1,..im; k = k1,…km, in 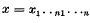 .
.