Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-26T02:05:09.776Z Has data issue: false hasContentIssue false
  • English
  • Français

Expansions in terms of Parabolic Cylinder Functions

Published online by Cambridge University Press:  20 January 2009

T. M. Cherry
T. M. Cherry
Affiliation:
The University, Melbourne, Australia.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

When the plane wave equation is expressed in terms of parabolic co-ordinates x, y, the variables are separable, and the elementary solutions have the form

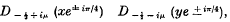
where x, y, μ are real. In this context, therefore, the functions Dν (z) which are directly significant are those where amp z = ± π/4 and ν + ½ is purely imaginary, rather than those where z is real and ν is a positive integer. The expansion of an arbitrary function in terms of the latter sort of D-function (substantially, in terms of Hermite polynomials) is well known. This paper is concerned with the expansion in terms of the former sort of D-function.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 8 , Issue 2 , October 1948 , pp. 50 - 65
Copyright
Copyright © Edinburgh Mathematical Society 1948

References

page 50 note 1 Magnus, W., Jahresbericht Deutsch. Math. Verein., 50 (1940), 140–161. The formula (A) was proved by A. Erdélyi about 1934, but was not published.Google Scholar

page 51 note 1 It is likely that the results (i), (ii) are not new, but I know of no reference; they may be proved from the formula

by the saddle-poinfc method. In Proc. London Math. Soc. (2), 17 (1918), 116, Watson proves results like (3), but his work does not cover the case where ampv is near ±½π. For (iii) see Whittaker and Watson, Modern Analysis (4th ed.) § 16.52.Google Scholar

page 57 note 1 Here, and below, the usual convention is made that an A or AN is not necessarily the same at each occurrence.

page 58 note 1 In fact, as in the proof of (31), the choice Ny = max(4y 6, 4x 6) is suitable, but no such explicit estimate is needed in the argument.

page 62 note 1 Proc. Roy. Soc. Edinburgh, 61 (1941), 61–70.Google Scholar

page 62 note 2 See, for example, Baker and Copson, The Mathematical Theory of Iluygens' Principle, Chap. IV; the function defined by (1.65) on p. 140 agrees, to a constant factor, with J as given by my equation (47).