No CrossRef data available.
Article contents
Equisingularity in pencils of curves on germs of reduced complex surfaces
Part of:
Local theory
Published online by Cambridge University Press: 04 June 2024
Abstract
We study pencils of curves on a germ of complex reduced surface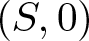 
$(S,0)$. These are families of curves parametrized by 
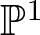$ \mathbb{P}^1 $ having 0 as the unique common point. We prove that for 
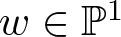$w\in \mathbb{P}^1$, the corresponding curve of the pencil does not have the generic topology if and only if either the corresponding curve of the pulled-back pencil to the normalized surface has a non generic topology or w is a limit value for the function 
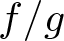$ f/g $ along the singular locus of 
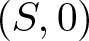$(S,0)$, where f and g are generators of the pencil.
MSC classification
Primary:
14B05: Singularities
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society.
References
Bondil, R. and D. T., Lê, Caractérisations des éléments superficiels d’un idéal, C. R. Acad. Sci., Paris, Sér. I, Math. 332 (8) (2001), 717–722.CrossRefGoogle Scholar
Brücker, C. and G.-M., Greuel, Deformationen isolierter Kurvensingularitäten mit eingebetteten Komponenten. (Deformations of isolated curve singularities with embedded components), Manuscr. Math. 70 (1) (1990), 93–114.CrossRefGoogle Scholar
Buchweitz, R.-O. and G.-M., Greuel, The Milnor number and deformations of complex curve singularities, Invent. Math. 58 (1980), 241–281.CrossRefGoogle Scholar
Decker, W., Greuel, G.-M., Pfister, G. and Schönemann, H., Singular 4-2-0 – A Computer Algebra System for Polynomial Computations. 2020, http://www.singular.uni-kl.de.Google Scholar
Delgado, F. and H., Maugendre, Special fibres and critical locus for a pencil of plane curve singularities, Compositio Math. 136 (1) (2003), 69–87.CrossRefGoogle Scholar
Delgado, F. and Maugendre, H., Pencils and critical loci on normal surfaces, Rev. Mat. Complut. 34 (3) (2021), 691–714.CrossRefGoogle Scholar
Fernández de Bobadilla, J., Snoussi, J. and Spivakovsky, M., Equisingularity in one-parameter families of generically reduced curves, Int. Math. Res. Not. 2017 (5) (2017), 1589–1609.Google Scholar
Giles Flores, A., Silva, O. N. and Snoussi, J., On tangency in equisingular families of curves and surfaces, Q. J. Math. 71(2) (2020), 485–505.Google Scholar
Greuel, G.-M., Equisingular and equinormalizable deformations of isolated non-normal singularities, Methods Appl. Anal. 24(2) (2017), 215–276.CrossRefGoogle Scholar
Greuel, G.-M., Lossen, C. and Shustin, E., Introduction to Singularities and Deformations, Springer, Berlin 2007.Google Scholar
Laufer, H. B., Normal Two-dimensional Singularities, 71. Princeton University Press Princeton, NJ 1971.Google Scholar
Lê, D. T., and C., Weber, Équisingularité dans les pinceaux de germes de courbes planes et 
$C^0$-suffisance, Enseign. Math. 43 (3–4) (1997), 355–380.Google Scholar
$C^0$-suffisance, Enseign. Math. 43 (3–4) (1997), 355–380.Google ScholarMatsumura, H., Commutative Ring Theory. Transl. From the Japanese by M. Reid, 8. Cambridge University Press, Cambridge, 1986.Google Scholar
Mumford, D., The topology of normal singularities of an algebraic surface and a criterion for simplicity, Publ. Math., Inst. Hautes Étud. Sci. 9 (1961), 5–22.CrossRefGoogle Scholar
Ngô Viêt, T. and Ikeda, S., When is the Rees algebra Cohen-Macaulay? Commun. Algebra 17 (12) (1989), 2893–2922.Google Scholar
Silva, O. N. and J., Snoussi, Whitney equisingularity in families of generically reduced curves, Manuscr. Math. 163 (3–4) (2020), 463–479.CrossRefGoogle Scholar
Snoussi, J., Limites d’espaces tangents à une surface normale. PhD thesis, Université de Provence France, 1998.CrossRefGoogle Scholar
Snoussi, J., Limites d’espaces tangents à une surface normale, Comment. Math. Helv. 76(1) (2001), 61–88.CrossRefGoogle Scholar