Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-28T06:04:56.622Z Has data issue: false hasContentIssue false
  • English
  • Français

The Equation of Telegraphy

Published online by Cambridge University Press:  20 January 2009

M. C. Gray
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The equation of the propagation of electric signals along cables, generally known as the equation of telegraphy, may be written

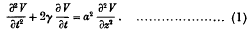
Particular solutions of this equation, adapted to various purposes have been found by Heaviside, Poincaré, A. G. Webster, T. W. Chaundy, § and others. The object of the present paper is to unify the theory of the equation by exhibiting the relations which these solutions bear to each other, and by obtaining them as particular cases of a general solution. The derivation of new particular solutions by the solution of integral equations is also discussed.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 42 , February 1923 , pp. 14 - 28
Copyright
Copyright © Edinburgh Mathematical Society 1923

References

* Electrical Papers, Vol, I., pp. 53 et seq. “On the Extra Current.”

† Comptes Rendus, 117 (1893), pp. 1027 et seq. “On the Propagation of Electricity.”

‡ “Electricity and Magnetism,” pp. 540 et seq.

§ Proc. London Math. Soc. (2) XXI. (1922), pp. 214–234.

* Cf. Riemann, Ges. Werke (1876), pp. 158 et seq.; or Darboux, Théorie Génerale des Surfaces, t. II., pp. 75 et seq.

* Nouveaux Mémoires de l'Acad. des Science, t. III.