Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-12-01T00:08:14.740Z Has data issue: false hasContentIssue false
  • English
  • Français

Enumeration of Indices of given Altitude and Potency

Published online by Cambridge University Press:  20 January 2009

H. Minc
H. Minc
Affiliation:
The University of British Columbia, Vancouver, Canada
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Indices of the free logarithmetic 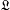correspond to bifurcating root-trees (cf.(4)), to Evans' non-associative numbers (3) and to Etherington's partitive numbers (2). The free commutative logarithmetic 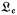is the homomorph of f 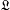determined by the congruence relation P + Q ∼ Q + P. Formulæ for aδ and pα, i.e. the numbers of indices of 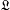of a given potency* δ and the number of indices of a given altitude α respectively, were given by Etherington (1), who also gave corresponding formulæ for commutative indices of 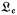. Other enumeration formulæ are contained in (5).

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 11 , Issue 4 , November 1959 , pp. 207 - 209
Copyright
Copyright © Edinburgh Mathematical Society 1959

References

REFERENCES

Etherington, I. M. H., On non-associative combinations, Proc. Roy. Soc Edin., 59 (1939), 153–162.CrossRefGoogle Scholar
Etherington, I. M. H., Non-associative arithmetics, Proc. Roy. Soc. Edin., A, 62 (1949), 442–453.Google Scholar
Evans, Trevor, Non-associative number theory, Amer. Math. Monthly, 64 (1957), 299–309.CrossRefGoogle Scholar
Mine, H., Index polynomials and bifurcating root-trees, Proc. Roy Soc. Edin., A, 64 (1957), 319–341.Google Scholar
Mine, H., The free commutative entropic logarithmetic, Proc. Roy. Soc. Edin., A, 65 (1959), 177–192.Google Scholar