Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-26T01:08:48.193Z Has data issue: false hasContentIssue false
  • English
  • Français

Enumeration of Indices of Given Altitude and Degree

Published online by Cambridge University Press:  20 January 2009

I. M. H. Etherington
I. M. H. Etherington
Affiliation:
Mathematical Institute, The University, Edinburgh
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

This note is a sequel to the article by Mine (2) on the same problem.

I described in (1) a notation for indices of powers in non-associative algebra, defined the degree † and altitude of a power or index, and observed that powers can be represented by bifurcating root-trees. For example, the power xx.x is denoted x2 + 1, with index 2 + 1, and is represented by the tree 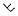; the degree (the number of factors, or free knots in the tree) is 3, and the altitude (the height of the tree) is 2. Multiplication being non-commutative or commutative, one maintains or ignores the distinction between left and right in the tree.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 12 , Issue 1 , June 1960 , pp. 1 - 5
Copyright
Copyright © Edinburgh Mathematical Society 1960

References

REFERENCES

(1)Etherington, I. M. H.On non-associative combinations, Proc. Roy. Soc. Edin., 59 (1939), 153–162.CrossRefGoogle Scholar
(2)Minc, H.Enumeration of indices of given altitude and potency, Proc. Edin. Math. Soc, 11 (1959), 207–209CrossRefGoogle Scholar