Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-26T00:43:29.692Z Has data issue: false hasContentIssue false
  • English
  • Français

Embeddings into finite idempotent-generated semigroups: some arithmetical results

Published online by Cambridge University Press:  20 January 2009

Emilia Giraldes  and
John M. Howie
Emilia Giraldes
Affiliation:
Universidade Nova de Lisboa
John M. Howie
Affiliation:
University of St Andrews
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A semiband is defined as a semigroup generated by idempotents. It is known that every finite semigroup is embeddable in a finite semiband. For a class C of semigroups and an integer n≧2, the number σC (n) is defined as the smallest k with the property that every semigroup of order n in the class C is embeddable in a semiband of order not exceeding k. It is shown that for the class Gp of groups σGp(n) = nq(ρGp(n)), where

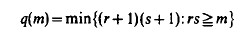
and

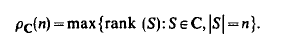
Estimates are known (and are quoted) for the function q. Estimates are considered for the function pC for various C

It is shown also that if C0S, CS denote respectively the classes of completely 0-simple and completely simple semigroups, then

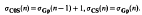
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 34 , Issue 2 , June 1991 , pp. 259 - 269
Copyright
Copyright © Edinburgh Mathematical Society 1991

References

REFERENCES

1.Benzaken, C. and Mayr, H. C., Notion de demi-bande: demi-bandes de type deux, Semigroup Forum 10 (1975), 115–125.CrossRefGoogle Scholar
2.Scares, Emilia Joaquina Giraldes, Semigrupos de caracteristica superior (Dissertaçāo de Doutoramente em Matemática, Universidade de Lisboa, 1984).Google Scholar
3.Giraldes, Emilia, Semigroups of high rank. II. Doubly noble semigroups, Proc. Edinburgh Math. Soc. 28 (1985), 409–417.CrossRefGoogle Scholar
4.Giraldes, Emilia and Howie, John M., Semigroups of high rank, Proc. Edinburgh Math. Soc. 28(1985), 13–34.CrossRefGoogle Scholar
5.Gomes, Gracinda M. S. and Howie, John M., On the ranks of certain semigroups of transformations, Math. Proc. Cambridge Philos. Soc. 101 (1987), 395–403.CrossRefGoogle Scholar
6.Howie, John M., The subsemigroup generated by the idempotents of a full transformation semigroup, J. London Math. Soc. 41 (1966), 707–716.CrossRefGoogle Scholar
7.Howie, John M., Idempotents in completely O-simple semigroups, Glasgow Math. J. 19 (1978), 109–113.CrossRefGoogle Scholar
8.Howie, John M., Embedding semigroups in semibands: some arithmetical results, Quart. J. Math. Oxford (2) 32 (1981), 323–337.CrossRefGoogle Scholar
9.Howie, John M. and Mcfadden, Robert B., Idempotent rank in finite full transformation semigroups, Proc. Roy. Soc. Edinburgh A 114 (1990), 161–167.CrossRefGoogle Scholar
10.Howie, John M. and Selfridge, J. L., A semigroup embedding problem and an arithmetical function, Math. Proc. Cambridge Philos. Soc., to appear.Google Scholar
11.Macdonald, Ian D., The theory of groups (Oxford, 1968).Google Scholar
12.Pastijn, Francis, Embedding semigroups in semibands, Semigroup Forum 14 (1977), 247–263.CrossRefGoogle Scholar
13.Tamura, T., Decompositions of a completely O-simple semigroup, Osaka J. Math. 12 (1960), 269–275.Google Scholar