Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-26T01:00:28.933Z Has data issue: false hasContentIssue false
  • English
  • Français

Distributive p-algebras and double p-algebras having n-permutable congruences

Published online by Cambridge University Press:  20 January 2009

R. Beazer
R. Beazer
Affiliation:
Department of MathematicsUniversity of GlasgowGlasgow, Scotland
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Recent research on aspects of distributive lattices, p-algebras, double p-algebras and de-Morgan algebras (see [2] and the references therein) has led to the consideration of the classes 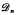(n≧1) of distributive lattices having no n + 1-element chain in their poset of prime ideals. In [1] we were obliged to characterize the members of 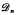by a sentence in the first-order theory of distributive lattices. Subsequently (see [2]), it was realised that 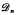coincides with the class of distributive lattices having n+1-permutable congruences. This result is hereby employed to describe those distributive p-algebras and double p-algebras having n-permutable congruences. As an application, new characterizations of those distributive p-algebras and double p-algebras having the property that their compact congruences are principal are obtained. In addition, those varieties of distributive p-algebras and double p-algebras having n-permutable congruences are announced.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 35 , Issue 2 , June 1992 , pp. 301 - 307
Copyright
Copyright © Edinburgh Mathematical Society 1992

References

REFERENCES

1.Adams, M. E. and Beazer, R., Congruence properties of distributive double p-algebras, Czechoslovak Math. J., 41 (1991), 216–231.CrossRefGoogle Scholar
2.Adams, M. E. and Beazer, R., Distributive lattices having n-permutable congruences, Proc. Amer. Math. Soc., to appear.Google Scholar
3.Balbes, R. and Dwinger, P., Distributive Lattices (University of Missouri Press, Columbia, Missouri, 1974).Google Scholar
4.Beazer, R., Principle congruence properties of some algebras with pseudocomplementation, Portugaliae Math., to appear.Google Scholar
5.Grätzer, G., General Lattice Theory (Birkhäuser, Basel and Stuttgart, 1978).CrossRefGoogle Scholar