Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-28T15:02:14.811Z Has data issue: false hasContentIssue false
  • English
  • Français

Distributive elements in centralizer near-rings

Published online by Cambridge University Press:  20 January 2009

C. J. Maxson  and
J. D. P. Meldrum
C. J. Maxson
Affiliation:
Mathematics Department, Texas A ' M University, College Station, Texas 77843, U.S.A.
J. D. P. Meldrum
Affiliation:
Mathematics Department, University of Edinburgh, Mayfield Road, Edinburgh EH9 3JZ, Scotland
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let <G,+> be a group with identity 0 and let S be a semigroup of endomorphisms of G. The set Ms(G)={f:G→G; f(0)=0, fσ=σf, for all σ∈S} with the operations of unction addition and composition is a zero-symmetric near-ring with identity called the centralizer near-ring determined by the pair (S, G). Centralizer near-rings have been studied for many classes of semigroups of endomorphisms. (See [8] and the references given there.) In this paper we continue these investigations into the structure of centralizer near-rings via our study of the relationship between distributive elements in Ms(G) and endomorphisms in Ms(G). More specifically, let N = Ms(G) and let Nd={f∈N; f(g1+g2)=fg1+fg2}, the set of distributive elements in N. Under the operation of function composition, Nd is a semigroup containing the identity map, id. Moreover, Nd contains as a submonoid 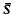= {α ∈ End G; ασ=σα for all σ∈S}. Here we determine for certain semigroups S, whether or not 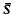= Nd.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 30 , Issue 3 , October 1987 , pp. 401 - 413
Copyright
Copyright © Edinburgh Mathematical Society 1987

References

REFERENCES

1.Betsch, G., Some structure theorems on 2-primitive near-rings, Colloq. Math. Soc. Janus Bolyai 6, Rings, Modules and Radicals (Keszthely (Hungary), 1971, North-Holland, 1973).Google Scholar
2.Maxson, C. J. and Smith, K. C., Simple near-ring centralizers of finite rings, Proc. Amer. Math. Soc. 75 (1979), 8–12.CrossRefGoogle Scholar
3.Maxson, C. J., and Smith, K. C., The centralizer of a set of group automorphisms, Comm. Algebra 8 (1980), 211–230.CrossRefGoogle Scholar
4.Maxson, C. J., and Smith, K. C., Centralizer near-rings that are endomorphism rings, Proc. Amer. Math. Soc. 80 (1980), 189–195.CrossRefGoogle Scholar
5.Mcdonald, B. R., Finite Rings with Identity (Dekker, N.Y., 1974).Google Scholar
6.Meldrum, J. D. P., On nilpotent wreath products, Proc. Cambridge Philos. Soc. 68 (1970), 1–15.CrossRefGoogle Scholar
7.Meldrum, J. D. P., Centralisers in wreath products, Proc. Edinburgh Math. Soc. 22 (1979), 161–168.CrossRefGoogle Scholar
8.Pilz, G., Near-rings (Revised Edition, North-Holland, Amsterdam, N.Y. and Oxford, 1983).Google Scholar
9.Robinson, D. J. S., A Course in the Theory of Groups (Grad. Texts in Math. 80, Springer, Berlin, 1982).CrossRefGoogle Scholar