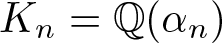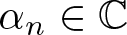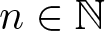1. Introduction and statements of results
The discriminant is a basic invariant associated with an algebraic number field. Its notion was first introduced by Dedekind in 1871. The problem of effective computation of discriminant as well as an integral basis of an infinite family of algebraic number fields which are defined over the field ![]() $\mathbb{Q}$ of rational numbers by certain types of irreducible polynomials has been tackled by several mathematicians (cf. [Reference Alaca1, Reference Alaca and Williams2, Reference Funakura7, Reference Kaur and Khanduja10, Reference Llorente, Nart and Vila15, Reference Llorente, Nart and Vila17, Reference Westlund21]). In this paper, we deal with the above problem for the family of exponential Taylor polynomials:
$\mathbb{Q}$ of rational numbers by certain types of irreducible polynomials has been tackled by several mathematicians (cf. [Reference Alaca1, Reference Alaca and Williams2, Reference Funakura7, Reference Kaur and Khanduja10, Reference Llorente, Nart and Vila15, Reference Llorente, Nart and Vila17, Reference Westlund21]). In this paper, we deal with the above problem for the family of exponential Taylor polynomials:
 \begin{equation*}
T_n(x)=\frac{x^n}{n!}+ \frac{x^{n-1}}{(n-1)!}+ \cdots +\frac{x^2}{2!}+\frac{x}{1!}+1,
\end{equation*}
\begin{equation*}
T_n(x)=\frac{x^n}{n!}+ \frac{x^{n-1}}{(n-1)!}+ \cdots +\frac{x^2}{2!}+\frac{x}{1!}+1,
\end{equation*} whose irreducibility over ![]() $\mathbb{Q}$ was proved by Schur in 1929 for
$\mathbb{Q}$ was proved by Schur in 1929 for ![]() $n \geq 1$ (see [Reference Coleman6, Reference Schur19, Reference Schur20]). Let Kn denote the algebraic number field
$n \geq 1$ (see [Reference Coleman6, Reference Schur19, Reference Schur20]). Let Kn denote the algebraic number field ![]() $\mathbb{Q}(\alpha_n)$, where
$\mathbb{Q}(\alpha_n)$, where ![]() $\alpha_n\in \mathbb{C}$ is a root of
$\alpha_n\in \mathbb{C}$ is a root of ![]() $T_n(x)$. In this paper, we calculate the discriminant of the field Kn and explicitly construct a p-integral basis (defined below) of Kn for each prime number p and
$T_n(x)$. In this paper, we calculate the discriminant of the field Kn and explicitly construct a p-integral basis (defined below) of Kn for each prime number p and ![]() $n\geq 1$. These p-integral bases quickly lead to the construction of an integral basis of Kn as illustrated in Example 5.2. Our proofs are theoretical without involving computer programming and we use several well-known basic results of algebraic number theory besides the Theorem of Index of Ore.
$n\geq 1$. These p-integral bases quickly lead to the construction of an integral basis of Kn as illustrated in Example 5.2. Our proofs are theoretical without involving computer programming and we use several well-known basic results of algebraic number theory besides the Theorem of Index of Ore.
We first introduce some notations. For an algebraic number field K, AK will stand for its ring of algebraic integers and dK for its discriminant. If ![]() $K=\mathbb{Q}(\theta)$ with θ an algebraic integer having minimal polynomial f(x) over
$K=\mathbb{Q}(\theta)$ with θ an algebraic integer having minimal polynomial f(x) over ![]() $\mathbb{Q}$, then the group index
$\mathbb{Q}$, then the group index ![]() $[A_K:\mathbb Z[\theta]]$ will be denoted by ind θ and the discriminant of the polynomial f(x) by discr(f). For a prime number p, by
$[A_K:\mathbb Z[\theta]]$ will be denoted by ind θ and the discriminant of the polynomial f(x) by discr(f). For a prime number p, by ![]() $\mathbb{Z}_{(p)}$ we shall denote the localisation of the ring
$\mathbb{Z}_{(p)}$ we shall denote the localisation of the ring ![]() $\mathbb{Z}$ at the prime ideal
$\mathbb{Z}$ at the prime ideal ![]() $p\mathbb{Z}$. If
$p\mathbb{Z}$. If ![]() $I_{(p)}$ stands for the integral closure of the ring
$I_{(p)}$ stands for the integral closure of the ring ![]() $\mathbb{Z}_{(p)}$ in an algebraic number field K, then
$\mathbb{Z}_{(p)}$ in an algebraic number field K, then ![]() $I_{(p)}=\{\frac{\alpha}{a}~|~\alpha\in A_K,~a\in \mathbb{Z}\setminus p\mathbb{Z}~\}$ is a free
$I_{(p)}=\{\frac{\alpha}{a}~|~\alpha\in A_K,~a\in \mathbb{Z}\setminus p\mathbb{Z}~\}$ is a free ![]() $\mathbb{Z}_{(p)}$-module of rank equal to the degree of the extension
$\mathbb{Z}_{(p)}$-module of rank equal to the degree of the extension ![]() $K/\mathbb{Q}$. A basis of
$K/\mathbb{Q}$. A basis of ![]() $I_{(p)}$ as a
$I_{(p)}$ as a ![]() $\mathbb{Z}_{(p)}$-module is called a p-integral basis of K. Note that if
$\mathbb{Z}_{(p)}$-module is called a p-integral basis of K. Note that if ![]() $K=\mathbb{Q}(\theta)$ with θ in AK and p is a prime number not dividing ind θ, then by Lagrange’s theorem for finite groups,
$K=\mathbb{Q}(\theta)$ with θ in AK and p is a prime number not dividing ind θ, then by Lagrange’s theorem for finite groups, ![]() $A_K \subseteq \mathbb{Z}_{(p)}[\theta]$ and hence
$A_K \subseteq \mathbb{Z}_{(p)}[\theta]$ and hence ![]() $I_{(p)}=\mathbb{Z}_{(p)}[\theta]$, i.e., {1,
$I_{(p)}=\mathbb{Z}_{(p)}[\theta]$, i.e., {1,![]() $\theta,\dots ,\theta^{n-1} $} is a p-integral basis of K, n being the degree of the extension
$\theta,\dots ,\theta^{n-1} $} is a p-integral basis of K, n being the degree of the extension ![]() $K/\mathbb{Q}$. Throughout vp will stand for the p-adic valuation of
$K/\mathbb{Q}$. Throughout vp will stand for the p-adic valuation of ![]() $\mathbb{Q} $ defined for any non-zero integer m to be the highest power of the prime p dividing m. For a real number λ, we shall denote by
$\mathbb{Q} $ defined for any non-zero integer m to be the highest power of the prime p dividing m. For a real number λ, we shall denote by ![]() $\lfloor {\lambda} \rfloor$ the largest integer not exceeding λ.
$\lfloor {\lambda} \rfloor$ the largest integer not exceeding λ.
With the above notations, we prove
Theorem 1.1. Let p be a prime number and let ![]() $n\geq 2$ be an integer having p-adic expansion:
$n\geq 2$ be an integer having p-adic expansion:
with ![]() $0\leq m_1 \lt m_2 \lt \cdots \lt m_s$ and
$0\leq m_1 \lt m_2 \lt \cdots \lt m_s$ and ![]() $0 \lt c_i \lt p$ for each i. Let
$0 \lt c_i \lt p$ for each i. Let ![]() $K = \mathbb{Q}(\theta)$ be an algebraic number field with θ a root of the irreducible polynomial
$K = \mathbb{Q}(\theta)$ be an algebraic number field with θ a root of the irreducible polynomial  $f_n(x)=x^n+ \frac{n!}{(n-1)!}x^{n-1}+ \cdots +\frac{n!}{2!}x^2+\frac{n!}{1!}x+n!$ belonging to
$f_n(x)=x^n+ \frac{n!}{(n-1)!}x^{n-1}+ \cdots +\frac{n!}{2!}x^2+\frac{n!}{1!}x+n!$ belonging to ![]() $\mathbb{Z}[x]$. Let dK stand for the discriminant of K and di for the integer
$\mathbb{Z}[x]$. Let dK stand for the discriminant of K and di for the integer  $\frac{p^{m_i}-1}{p-1}$. Then
$\frac{p^{m_i}-1}{p-1}$. Then ![]() $v_p({\rm ind}\ \theta)$ and
$v_p({\rm ind}\ \theta)$ and ![]() $v_p(d_K)$ are given by:
$v_p(d_K)$ are given by:
 \begin{align}
v_p({\rm ind}\ \theta)
&=\frac 12
\sum\limits_{i=1}^{s}[c_id_i\left(c_ip^{m_i}+2c_{i+1}p^{m_{i+1}}+\cdots+2c_sp^{m_s}-p\right) ],
\end{align}
\begin{align}
v_p({\rm ind}\ \theta)
&=\frac 12
\sum\limits_{i=1}^{s}[c_id_i\left(c_ip^{m_i}+2c_{i+1}p^{m_{i+1}}+\cdots+2c_sp^{m_s}-p\right) ],
\end{align} \begin{align}
v_p(d_K) &=p\sum\limits_{i=1}^{s} c_id_i+\sum\limits_{1\leqslant i \lt j\leqslant s} \frac{c_ic_j(p^{m_j}-p^{m_i})}{p-1}.
\end{align}
\begin{align}
v_p(d_K) &=p\sum\limits_{i=1}^{s} c_id_i+\sum\limits_{1\leqslant i \lt j\leqslant s} \frac{c_ic_j(p^{m_j}-p^{m_i})}{p-1}.
\end{align}The following corollaries will be quickly deduced from the above theorem.
Corollary 1.2. Let n and ![]() $K=\mathbb{Q}(\theta)$ be as in the above theorem. Then a prime number p divides
$K=\mathbb{Q}(\theta)$ be as in the above theorem. Then a prime number p divides ![]() $[ A_K:\mathbb{Z}[\theta]]$ if and only if p 2 divides
$[ A_K:\mathbb{Z}[\theta]]$ if and only if p 2 divides ![]() $n!$. In particular,
$n!$. In particular, ![]() $A_K=\mathbb{Z}[\theta]$ if and only if n is 2 or 3.
$A_K=\mathbb{Z}[\theta]$ if and only if n is 2 or 3.
Corollary 1.3. With notations as in the above corollary, a prime number p divides dK if and only if p divides ![]() $n!$.
$n!$.
Recall that for a non-zero polynomial  $g(x)=\sum\limits_{i=0}^{n}a_ix^i \in \mathbb{Z}[x]$ with
$g(x)=\sum\limits_{i=0}^{n}a_ix^i \in \mathbb{Z}[x]$ with ![]() $a_0a_n\ne0$, the Newton polygon of g(x) with respect to a prime number p is the polygonal path along the lower convex hull of the points in the set
$a_0a_n\ne0$, the Newton polygon of g(x) with respect to a prime number p is the polygonal path along the lower convex hull of the points in the set ![]() $\{(i, v_p(a_{n-i}))~|~ 0\leq i \leq n,~ a_{n-i}\ne 0 \}$ (see Definition 2.1).
$\{(i, v_p(a_{n-i}))~|~ 0\leq i \leq n,~ a_{n-i}\ne 0 \}$ (see Definition 2.1).
Theorem 1.4. Let ![]() $K = \mathbb{Q}(\theta)$ and
$K = \mathbb{Q}(\theta)$ and ![]() $f_n(x)$ be as in Theorem 1.1 and let p be a prime number. For any integer j with
$f_n(x)$ be as in Theorem 1.1 and let p be a prime number. For any integer j with ![]() $1\leq j \leq n-1$, let
$1\leq j \leq n-1$, let ![]() $u_j(x)$ denote the polynomial
$u_j(x)$ denote the polynomial  $x^{j}+\frac{n!}{(n-1)!}x^{j-1}+\cdots+\frac{n!}{(n-j)!}$ with coefficients in
$x^{j}+\frac{n!}{(n-1)!}x^{j-1}+\cdots+\frac{n!}{(n-j)!}$ with coefficients in ![]() $\mathbb{Z}$. Then a p-integral basis of K is given by
$\mathbb{Z}$. Then a p-integral basis of K is given by ![]() $\{1, \beta_1, \cdots, \beta_{n-1}\}$ with
$\{1, \beta_1, \cdots, \beta_{n-1}\}$ with  $\beta_j=\frac{u_j(\theta)} {p^{\lfloor y_j\rfloor}}$ for
$\beta_j=\frac{u_j(\theta)} {p^{\lfloor y_j\rfloor}}$ for ![]() $1\leq j \leq n-1$, where yj stands for the ordinate of the point with abscissa j on the Newton polygon of
$1\leq j \leq n-1$, where yj stands for the ordinate of the point with abscissa j on the Newton polygon of ![]() $f_n(x)$ with respect to the prime p.
$f_n(x)$ with respect to the prime p.
The following theorem proved in [Reference Kaur and Khanduja10, Theorem 1.2] gives a method to construct an integral basis of an algebraic number field using its p-integral bases.
Theorem 1.A.
Let ![]() $L=\mathbb{Q}(\xi)$ be an algebraic number field of degree n with ξ an algebraic integer. Let
$L=\mathbb{Q}(\xi)$ be an algebraic number field of degree n with ξ an algebraic integer. Let ![]() $p_1,\dots ,p_s$ be all the prime numbers dividing
$p_1,\dots ,p_s$ be all the prime numbers dividing ![]() ${\rm ind}~\xi$ and
${\rm ind}~\xi$ and ![]() $\{1,\alpha_{r1},\dots,\alpha_{r(n-1)}\}$ be a pr-integral basis of L,
$\{1,\alpha_{r1},\dots,\alpha_{r(n-1)}\}$ be a pr-integral basis of L, ![]() $1 \leq r\leq s $ with:
$1 \leq r\leq s $ with:
 \begin{align*}
\alpha_{ri}=\frac{c_{i0}^{(r)}+c_{i1}^{(r)}\xi+\cdots+c_{i(i-1)}^{(r)}\xi^{i-1}+\xi^i}{p_r^{k_{i,r}}},\quad 1\leq i \leq n-1,
\end{align*}
\begin{align*}
\alpha_{ri}=\frac{c_{i0}^{(r)}+c_{i1}^{(r)}\xi+\cdots+c_{i(i-1)}^{(r)}\xi^{i-1}+\xi^i}{p_r^{k_{i,r}}},\quad 1\leq i \leq n-1,
\end{align*} where  $c_{ij}^{(r)}$ and
$c_{ij}^{(r)}$ and ![]() $ 0\leq k_{i,r}\leq k_{i+1,r}$ are integers. If
$ 0\leq k_{i,r}\leq k_{i+1,r}$ are integers. If ![]() $c_{ij} \in \mathbb{Z}$ are such that
$c_{ij} \in \mathbb{Z}$ are such that  $c_{ij} \equiv c_{ij}^{(r)} \pmod {p_r^{k_{i,r}} }$ for
$c_{ij} \equiv c_{ij}^{(r)} \pmod {p_r^{k_{i,r}} }$ for ![]() $1 \leq r\leq s $ and if ti stands for
$1 \leq r\leq s $ and if ti stands for  $\displaystyle \prod_{r=1}^{s} p_r^{k_{i,r}}$, then
$\displaystyle \prod_{r=1}^{s} p_r^{k_{i,r}}$, then ![]() $\{1,\alpha_1,\dots,\alpha_{n-1}\}$ is an integral basis of L where
$\{1,\alpha_1,\dots,\alpha_{n-1}\}$ is an integral basis of L where
 \begin{align*}
\alpha_i=\frac{c_{i0}+c_{i1}\xi+\cdots+c_{i(i-1)}\xi^{i-1}+\xi^i}{t_{i}},\quad 1\leq i\leq n-1.
\end{align*}
\begin{align*}
\alpha_i=\frac{c_{i0}+c_{i1}\xi+\cdots+c_{i(i-1)}\xi^{i-1}+\xi^i}{t_{i}},\quad 1\leq i\leq n-1.
\end{align*} It may be pointed out that for any algebraic number field ![]() $L=\mathbb{Q}(\xi)$, a p-integral basis of the type given in the above theorem always exists for each prime p in view of [Reference Khanduja11, Theorem 2.34]. We shall illustrate Theorems 1.4 and Theorem 1.A by constructing an explicit integral basis of
$L=\mathbb{Q}(\xi)$, a p-integral basis of the type given in the above theorem always exists for each prime p in view of [Reference Khanduja11, Theorem 2.34]. We shall illustrate Theorems 1.4 and Theorem 1.A by constructing an explicit integral basis of ![]() $K=\mathbb{Q}(\theta)$ when θ is a root of
$K=\mathbb{Q}(\theta)$ when θ is a root of ![]() $f_6(x)$ or
$f_6(x)$ or ![]() $f_7(x)$ in Example 5.2.
$f_7(x)$ in Example 5.2.
2. Preliminary results
The following lemma is essentially proved in [Reference Coleman6, p. 187]. For reader’s convenience, we prove it here.
Lemma 2.A.
Let ![]() $n \geq 2$ be an integer. Then the discriminant of the polynomial
$n \geq 2$ be an integer. Then the discriminant of the polynomial  $f_n(x)=x^n+ \frac{n!}{(n-1)!}x^{n-1}+ \cdots +\frac{n!}{2!}x^2+\frac{n!}{1!}x+n!$ is
$f_n(x)=x^n+ \frac{n!}{(n-1)!}x^{n-1}+ \cdots +\frac{n!}{2!}x^2+\frac{n!}{1!}x+n!$ is  $(-1)^{\frac{n(n-1)}{2}} (n!)^{n}.$
$(-1)^{\frac{n(n-1)}{2}} (n!)^{n}.$
Proof. It can be easily seen that:
 \begin{equation}
f_n^{'}(x)=nf_{n-1}(x), \quad
f_n(x)=x^n+nf_{n-1}(x).
\end{equation}
\begin{equation}
f_n^{'}(x)=nf_{n-1}(x), \quad
f_n(x)=x^n+nf_{n-1}(x).
\end{equation} Let ![]() $\beta_1, \beta_2, \dots, \beta_n$ be the roots of
$\beta_1, \beta_2, \dots, \beta_n$ be the roots of ![]() $f_n(x)$ in
$f_n(x)$ in ![]() $\mathbb{C}$. Then the discriminant of
$\mathbb{C}$. Then the discriminant of ![]() $f_n(x)$ is given by:
$f_n(x)$ is given by:
 \begin{equation*}
discr (f_n)=(-1)^{\frac{n(n-1)}{2}} \prod\limits_{j=1}^{n} f_n^{'}(\beta_{j}).
\end{equation*}
\begin{equation*}
discr (f_n)=(-1)^{\frac{n(n-1)}{2}} \prod\limits_{j=1}^{n} f_n^{'}(\beta_{j}).
\end{equation*}Therefore using (3), we see that:
 \begin{align*}
discr (f_n)&=(-1)^{\frac{n(n-1)}{2}} \prod\limits_{j=1}^{n} \left(nf_{n-1}(\beta_{j})\right)
= (-1)^{\frac{n(n-1)}{2}}\prod\limits_{j=1}^{n} \left( -\beta_{j}^n \right)
=(-1)^{\frac{n(n-1)}{2}} (n!)^{n}.
\end{align*}
\begin{align*}
discr (f_n)&=(-1)^{\frac{n(n-1)}{2}} \prod\limits_{j=1}^{n} \left(nf_{n-1}(\beta_{j})\right)
= (-1)^{\frac{n(n-1)}{2}}\prod\limits_{j=1}^{n} \left( -\beta_{j}^n \right)
=(-1)^{\frac{n(n-1)}{2}} (n!)^{n}.
\end{align*}The following simple result is well known (see [Reference Burton3, p. 122], [Reference Coleman6]). Its proof is omitted.
Lemma 2.B.
Let p be a prime number and m be a positive integer. If ![]() $m=a_0+a_1p+\cdots+a_rp^r$ with
$m=a_0+a_1p+\cdots+a_rp^r$ with ![]() $0\leq a_i \lt p$ for each i, then
$0\leq a_i \lt p$ for each i, then
 \begin{align*}
v_p(m!)=\frac{m-(a_0+a_1+\cdots+a_r)}{p-1}.
\end{align*}
\begin{align*}
v_p(m!)=\frac{m-(a_0+a_1+\cdots+a_r)}{p-1}.
\end{align*}The elementary lemma stated below is also well known (cf. [Reference de Koninck and Mercier14, Problem 435]).
Lemma 2.C.
Let ![]() $t, n$ be positive integers. Let
$t, n$ be positive integers. Let ![]() $\mathcal P$ denote the set of points in the plane with positive integer entries lying inside or on the triangle with vertices
$\mathcal P$ denote the set of points in the plane with positive integer entries lying inside or on the triangle with vertices ![]() $(0,0), (n, 0), (n,t)$ which do not lie on the line x = n. Then the number of elements in
$(0,0), (n, 0), (n,t)$ which do not lie on the line x = n. Then the number of elements in ![]() $\mathcal P$ is
$\mathcal P$ is  $\frac{1}{2} [(n-1)(t-1) + \gcd(t, n) -1].$
$\frac{1}{2} [(n-1)(t-1) + \gcd(t, n) -1].$
For proving Theorem 1.1, we will use the classical Theorem of Index of Ore (stated as Theorem 2.E below) in addition to carrying out several simplifications. To state this theorem, we introduce the notions of valuation, Gauss valuation, ϕ-Newton polygon, ϕ-index of a polynomial, where ![]() $\phi(x)$ belonging to
$\phi(x)$ belonging to ![]() $\mathbb{Z}[x]$ is a monic polynomial which is irreducible modulo a given prime p.
$\mathbb{Z}[x]$ is a monic polynomial which is irreducible modulo a given prime p.
As usual, by a valuation v of a field K, we shall mean a mapping ![]() $v:K \longrightarrow\mathbb{R}\cup \{\infty\}$ which satisfies the following properties for all
$v:K \longrightarrow\mathbb{R}\cup \{\infty\}$ which satisfies the following properties for all ![]() $\alpha,~\beta$ in K.
$\alpha,~\beta$ in K.
(i) ![]() $v(\alpha)= \infty$ if and only if
$v(\alpha)= \infty$ if and only if ![]() $\alpha=0,$
$\alpha=0,$
(ii) ![]() $v(\alpha\beta)= v(\alpha)+ v(\beta)$,
$v(\alpha\beta)= v(\alpha)+ v(\beta)$,
(iii) ![]() $v(\alpha+\beta)\geq $ min
$v(\alpha+\beta)\geq $ min![]() $\{v(\alpha), v(\beta)\}.$
$\{v(\alpha), v(\beta)\}.$
The subring Rv of K defined by ![]() ${R}_v= \left\lbrace \alpha\in K\mid v(\alpha)\geq 0\right\rbrace $ is called the valuation ring of v. It has a unique maximal ideal
${R}_v= \left\lbrace \alpha\in K\mid v(\alpha)\geq 0\right\rbrace $ is called the valuation ring of v. It has a unique maximal ideal ![]() $\mathcal {M}_v=\left\lbrace \alpha\in K\mid v(\alpha) \gt 0\right\rbrace $ and
$\mathcal {M}_v=\left\lbrace \alpha\in K\mid v(\alpha) \gt 0\right\rbrace $ and ![]() ${R}_v/\mathcal{M}_v$ is called the residue field of v. A valuation vʹ of an overfield Kʹ of K is said to be an extension or a prolongation of v to Kʹ if vʹ coincides with v on K.
${R}_v/\mathcal{M}_v$ is called the residue field of v. A valuation vʹ of an overfield Kʹ of K is said to be an extension or a prolongation of v to Kʹ if vʹ coincides with v on K.
Notations. For a prime number p, as usual ![]() $\mathbb{Z}_p$ will stand for the ring of p-adic integers and
$\mathbb{Z}_p$ will stand for the ring of p-adic integers and ![]() $\mathbb{Q}_p$ for its quotient field. We shall also denote by vp the unique prolongation of the p-adic valuation to the field
$\mathbb{Q}_p$ for its quotient field. We shall also denote by vp the unique prolongation of the p-adic valuation to the field ![]() $\mathbb{Q}_p$ of p-adic numbers. If v 1 denotes the prolongation of vp to a finite extension of
$\mathbb{Q}_p$ of p-adic numbers. If v 1 denotes the prolongation of vp to a finite extension of ![]() $\mathbb{Q}_p$, then for any polynomial
$\mathbb{Q}_p$, then for any polynomial ![]() $g_1(x)$ with coefficients in the valuation ring of v 1,
$g_1(x)$ with coefficients in the valuation ring of v 1, ![]() $\overline{g}_1(x)$ will stand for the polynomial obtained by replacing each coefficient of
$\overline{g}_1(x)$ will stand for the polynomial obtained by replacing each coefficient of ![]() $g_1(x)$ by its image under the canonical homomorphism from the valuation ring of v 1 onto its residue field.
$g_1(x)$ by its image under the canonical homomorphism from the valuation ring of v 1 onto its residue field.
We shall denote by ![]() $v_p^x$ the Gaussian valuation of the field
$v_p^x$ the Gaussian valuation of the field ![]() $\mathbb{Q}_p(x)$ of rational functions in an indeterminate x which extends the valuation vp of
$\mathbb{Q}_p(x)$ of rational functions in an indeterminate x which extends the valuation vp of ![]() $\mathbb{Q}_p$ and is defined on
$\mathbb{Q}_p$ and is defined on ![]() $\mathbb{Q}_p[x]$ by:
$\mathbb{Q}_p[x]$ by:
 \begin{equation*}
v_p^x\left(\sum\limits_{i}c_ix^i\right)=\min_{i}\{v_p(c_i)\},\,\, \ c_i\in \mathbb{Q}_p.
\end{equation*}
\begin{equation*}
v_p^x\left(\sum\limits_{i}c_ix^i\right)=\min_{i}\{v_p(c_i)\},\,\, \ c_i\in \mathbb{Q}_p.
\end{equation*} If ![]() $\phi(x)$ is a fixed monic polynomial with coefficients in an integral domain R, then any polynomial
$\phi(x)$ is a fixed monic polynomial with coefficients in an integral domain R, then any polynomial ![]() $g(x)\in R[x]$ can be uniquely written as a finite sum
$g(x)\in R[x]$ can be uniquely written as a finite sum  $\sum\limits_{i}g_i(x)\phi(x)^i$ with
$\sum\limits_{i}g_i(x)\phi(x)^i$ with ![]() $\deg g_i(x) \lt \deg \phi(x)$ for each i; this expansion will be referred to as the ϕ-expansion of g(x).
$\deg g_i(x) \lt \deg \phi(x)$ for each i; this expansion will be referred to as the ϕ-expansion of g(x).
The following definition extends the notion of Newton polygon of a polynomial with respect to a prime p.
Definition 2.1. Let ![]() $\phi(x)\in \mathbb{Z}[x]$ be a monic polynomial which is irreducible modulo a given prime p. Let g(x) belonging to
$\phi(x)\in \mathbb{Z}[x]$ be a monic polynomial which is irreducible modulo a given prime p. Let g(x) belonging to ![]() $\mathbb{Z}_p[x]$ be a polynomial having ϕ-expansion
$\mathbb{Z}_p[x]$ be a polynomial having ϕ-expansion  $\sum\limits_{i=0}^{n}g_i(x) \phi(x)^i$ with
$\sum\limits_{i=0}^{n}g_i(x) \phi(x)^i$ with ![]() $g_0(x)g_n(x) \neq 0$. Let Pi stand for the point in the plane having coordinates
$g_0(x)g_n(x) \neq 0$. Let Pi stand for the point in the plane having coordinates ![]() $(i, v_p^x(g_{n-i}(x)))$ when
$(i, v_p^x(g_{n-i}(x)))$ when ![]() $g_{n-i}(x)\ne 0$,
$g_{n-i}(x)\ne 0$, ![]() $0\leq i \leq n$. Let µij denote the slope of the line joining the points Pi and Pj if
$0\leq i \leq n$. Let µij denote the slope of the line joining the points Pi and Pj if ![]() $g_{n-i}(x)g_{n-j}(x)\ne 0$. Let i 1 be the largest index
$g_{n-i}(x)g_{n-j}(x)\ne 0$. Let i 1 be the largest index ![]() $0 \lt i_1 \leq n$ such that:
$0 \lt i_1 \leq n$ such that:
If ![]() $i_1 \lt n$, let i 2 be the largest index
$i_1 \lt n$, let i 2 be the largest index ![]() $i_1 \lt i_2 \leq n$ satisfying:
$i_1 \lt i_2 \leq n$ satisfying:
and so on. The ϕ-Newton polygon of g(x) with respect to p is the polygonal path having segments ![]() $P_0P_{i_1}, P_{i_1}P_{i_2}, \dots, P_{i_{k-1}}P_{i_k}$ with
$P_0P_{i_1}, P_{i_1}P_{i_2}, \dots, P_{i_{k-1}}P_{i_k}$ with ![]() $i_k=n$. These segments are called the edges of the ϕ-Newton polygon of g(x) and their slopes from left to right form a strictly increasing sequence. In particular when
$i_k=n$. These segments are called the edges of the ϕ-Newton polygon of g(x) and their slopes from left to right form a strictly increasing sequence. In particular when ![]() $\phi(x)=x$, the ϕ-Newton polygon of g(x) with respect to p will be referred to as the Newton polygon of g(x) with respect to p.
$\phi(x)=x$, the ϕ-Newton polygon of g(x) with respect to p will be referred to as the Newton polygon of g(x) with respect to p.
Definition 2.2. Let ![]() $\phi(x)$ and g(x) be as in Definition 2.1. Let N denote the number of points with positive integer coordinates lying on or below the ϕ-Newton polygon of g(x) away from the vertical line passing through the last vertex of this polygon. As in [Reference Khanduja and Kumar13], the ϕ-index of g (with respect to p) is defined to be
$\phi(x)$ and g(x) be as in Definition 2.1. Let N denote the number of points with positive integer coordinates lying on or below the ϕ-Newton polygon of g(x) away from the vertical line passing through the last vertex of this polygon. As in [Reference Khanduja and Kumar13], the ϕ-index of g (with respect to p) is defined to be ![]() $N\deg \phi(x)$ and will be denoted by
$N\deg \phi(x)$ and will be denoted by ![]() $i_{\phi}(g)$.
$i_{\phi}(g)$.
The following example illustrates the above definition.
Example 2.3. Let  $ g(x)=f_4(x)=x^4+\frac{4!}{3!}x^3 +\frac{4!}{2!}x^2 +\frac{4!}{1!}x +4!.$ Consider
$ g(x)=f_4(x)=x^4+\frac{4!}{3!}x^3 +\frac{4!}{2!}x^2 +\frac{4!}{1!}x +4!.$ Consider ![]() $\phi(x)=x$. Note that the ϕ-Newton polygon of g(x) with respect to the prime 2 being the lower convex hull of the points
$\phi(x)=x$. Note that the ϕ-Newton polygon of g(x) with respect to the prime 2 being the lower convex hull of the points ![]() $(0, 0), (1, 2), (2, 2), (3,3)$ and
$(0, 0), (1, 2), (2, 2), (3,3)$ and ![]() $(4, 3)$ consists of a single edge joining the point
$(4, 3)$ consists of a single edge joining the point ![]() $(0, 0)$ with
$(0, 0)$ with ![]() $(4, 3)$. Thus
$(4, 3)$. Thus ![]() $i_{\phi}(g)=3$ (with respect to 2). Next consider
$i_{\phi}(g)=3$ (with respect to 2). Next consider ![]() $\phi_1(x)=x+1$. It can be easily checked that
$\phi_1(x)=x+1$. It can be easily checked that ![]() $g(x)= (x+1)^4+6(x+1)^2+8(x+1)+9$. So the ϕ 1-Newton polygon of g(x) with respect to 3 being the lower convex hull of the points
$g(x)= (x+1)^4+6(x+1)^2+8(x+1)+9$. So the ϕ 1-Newton polygon of g(x) with respect to 3 being the lower convex hull of the points ![]() $(0, 0), (2, 1), (3,0)$ and
$(0, 0), (2, 1), (3,0)$ and ![]() $(4, 2)$ consists of two edges; the first edge joins the point
$(4, 2)$ consists of two edges; the first edge joins the point ![]() $(0, 0)$ with
$(0, 0)$ with ![]() $(3, 0)$ and the second edge is the line segment joining the points
$(3, 0)$ and the second edge is the line segment joining the points ![]() $(3,0)$ and
$(3,0)$ and ![]() $(4, 2)$. Thus
$(4, 2)$. Thus ![]() $i_{\phi_1}(g)=0$ (with respect to 3).
$i_{\phi_1}(g)=0$ (with respect to 3).
We now state a theorem originally proved by Ore (see [Reference Khanduja and Kumar13, Theorem 1.2], [Reference Ore18]).
Theorem 2.D.
Let ![]() $L=\mathbb{Q}(\xi)$ be an algebraic number field with ξ satisfying a monic irreducible polynomial
$L=\mathbb{Q}(\xi)$ be an algebraic number field with ξ satisfying a monic irreducible polynomial ![]() $g(x) \in \mathbb{Z}[x]$ and p be a prime number. Let
$g(x) \in \mathbb{Z}[x]$ and p be a prime number. Let ![]() $ \overline{\phi}_{1}(x)^{e_1}\cdots\overline{\phi}_r{(x)}^{e_r}$ be the factorization of
$ \overline{\phi}_{1}(x)^{e_1}\cdots\overline{\phi}_r{(x)}^{e_r}$ be the factorization of ![]() ${g}(x)$ modulo p into a product of powers of distinct irreducible polynomials over the finite field
${g}(x)$ modulo p into a product of powers of distinct irreducible polynomials over the finite field ![]() $\mathbb{F}_p$ of p elements, where each
$\mathbb{F}_p$ of p elements, where each ![]() $\phi_i(x) \neq g(x)$ belonging to
$\phi_i(x) \neq g(x)$ belonging to ![]() $\mathbb{Z}[x]$ is monic. Then,
$\mathbb{Z}[x]$ is monic. Then,  $v_p({\rm ind}~\xi) \geq \sum\limits_{j=1}^{r}i_{\phi_j}(g).$
$v_p({\rm ind}~\xi) \geq \sum\limits_{j=1}^{r}i_{\phi_j}(g).$
Ore also gave a sufficient condition so that the inequality in the above theorem becomes equality. For this, he associated with each edge Sij of the ϕi-Newton polygon of g(x) having positive slope, a polynomial ![]() $T_{ij}(Y)$ in an indeterminate Y with coefficients from the field
$T_{ij}(Y)$ in an indeterminate Y with coefficients from the field ![]() $\mathbb F_q$ having
$\mathbb F_q$ having ![]() $q=p^{deg\phi_i(x)}$ elements described in the following definitions.
$q=p^{deg\phi_i(x)}$ elements described in the following definitions.
Definition 2.4. Let ![]() $\phi(x) \in\mathbb{Z}[x]$ be a monic polynomial which is irreducible modulo a given prime p having a root α in a finite extension of
$\phi(x) \in\mathbb{Z}[x]$ be a monic polynomial which is irreducible modulo a given prime p having a root α in a finite extension of ![]() $\mathbb{Q}_p$. Let
$\mathbb{Q}_p$. Let ![]() $g(x) \in \mathbb{Z}_p[x]$ be a monic polynomial not divisible by
$g(x) \in \mathbb{Z}_p[x]$ be a monic polynomial not divisible by ![]() $\phi(x)$ with ϕ-expansion
$\phi(x)$ with ϕ-expansion ![]() $\phi(x)^n + g_{n-1}(x)\phi(x)^{n-1} + \cdots + g_0(x)$ such that
$\phi(x)^n + g_{n-1}(x)\phi(x)^{n-1} + \cdots + g_0(x)$ such that ![]() $\overline{g}(x)$ is a power of
$\overline{g}(x)$ is a power of ![]() $\overline{\phi}(x)$. Suppose that the ϕ-Newton polygon of g(x) consists of a single edge, say S having positive slope denoted by
$\overline{\phi}(x)$. Suppose that the ϕ-Newton polygon of g(x) consists of a single edge, say S having positive slope denoted by ![]() $\frac{d}{e}$ with integers
$\frac{d}{e}$ with integers ![]() $d, e$ coprime, i.e.,
$d, e$ coprime, i.e.,  $\min\{\frac{v_p^x(g_{n-i}(x))}{i}~\mid~1\leq i\leq n\} = \frac{v_p^x(g_0(x))}{n} = \frac{d}{e}$ so that n is divisible by e, say n = et and
$\min\{\frac{v_p^x(g_{n-i}(x))}{i}~\mid~1\leq i\leq n\} = \frac{v_p^x(g_0(x))}{n} = \frac{d}{e}$ so that n is divisible by e, say n = et and ![]() $v_p^x(g_{n-ej}(x)) \geq dj$ for
$v_p^x(g_{n-ej}(x)) \geq dj$ for ![]() $1\leq j\leq t$. Thus the polynomial
$1\leq j\leq t$. Thus the polynomial  $h_j(x):=\frac{g_{n-ej}(x)}{p^{dj}}$ has coefficients in
$h_j(x):=\frac{g_{n-ej}(x)}{p^{dj}}$ has coefficients in ![]() $\mathbb{Z}_p$ and hence
$\mathbb{Z}_p$ and hence ![]() $h_j(\alpha)\in \mathbb{Z}_p[\alpha]$ for
$h_j(\alpha)\in \mathbb{Z}_p[\alpha]$ for ![]() $1\leq j \leq t$. The polynomial T(Y) in an indeterminate Y defined by
$1\leq j \leq t$. The polynomial T(Y) in an indeterminate Y defined by  $T(Y) = Y^t + \sum\limits_{j=1}^{t} \overline{h_j}(\overline{\alpha})Y^{t-j}$ having coefficients in
$T(Y) = Y^t + \sum\limits_{j=1}^{t} \overline{h_j}(\overline{\alpha})Y^{t-j}$ having coefficients in ![]() $\mathbb{F}_p[\overline{\alpha}]$ is said to be the polynomial associated to g(x) with respect to
$\mathbb{F}_p[\overline{\alpha}]$ is said to be the polynomial associated to g(x) with respect to ![]() $(\phi,S)$.
$(\phi,S)$.
The example given below illustrates the above definition.
Example 2.5. Let  $g(x)=f_4(x)=x^4+\frac{4!}{3!}x^3 +\frac{4!}{2!}x^2 +\frac{4!}{1!}x +4!.$ Clearly
$g(x)=f_4(x)=x^4+\frac{4!}{3!}x^3 +\frac{4!}{2!}x^2 +\frac{4!}{1!}x +4!.$ Clearly ![]() $g(x)\equiv x^4 \pmod 2$. Consider
$g(x)\equiv x^4 \pmod 2$. Consider ![]() $\phi(x)=x$. One can check that the ϕ-Newton polygon of g(x) with respect to the prime 2 consists of a single edge S joining the points
$\phi(x)=x$. One can check that the ϕ-Newton polygon of g(x) with respect to the prime 2 consists of a single edge S joining the points ![]() $(0, 0)$ and
$(0, 0)$ and ![]() $(4, 3)$. With notations as in the above definition, we see that d = 3, e = 4 and the polynomial associated to g(x) with respect to
$(4, 3)$. With notations as in the above definition, we see that d = 3, e = 4 and the polynomial associated to g(x) with respect to ![]() $(\phi,S)$ is
$(\phi,S)$ is ![]() $T(Y)=Y+\overline{1}$ belonging to
$T(Y)=Y+\overline{1}$ belonging to ![]() $\mathbb{F}_2[Y]$.
$\mathbb{F}_2[Y]$.
We now extend the notion of associated polynomial when g(x) is more general.
Definition 2.6. Let ![]() $p, \phi(x)$ and α be as in Definition 2.4. Let
$p, \phi(x)$ and α be as in Definition 2.4. Let ![]() $G(x)\in \mathbb{Z}_p[x]$ be a monic polynomial not divisible by
$G(x)\in \mathbb{Z}_p[x]$ be a monic polynomial not divisible by ![]() $\phi(x)$ such that
$\phi(x)$ such that ![]() $\overline{G}(x)$ is a power of
$\overline{G}(x)$ is a power of ![]() $\overline{\phi}(x)$. Let
$\overline{\phi}(x)$. Let ![]() $\lambda_1 \lt \cdots \lt \lambda_k$ be the slopes of the edges of the ϕ-Newton polygon of G(x) and Si denote the edge with slope λi. In view of the Theorem of Product by Ore (cf. [Reference Cohen, Movahhedi and Salinier5, Theorem 1.5], [Reference Khanduja and Kumar12, Theorem 1.1]), we can write
$\lambda_1 \lt \cdots \lt \lambda_k$ be the slopes of the edges of the ϕ-Newton polygon of G(x) and Si denote the edge with slope λi. In view of the Theorem of Product by Ore (cf. [Reference Cohen, Movahhedi and Salinier5, Theorem 1.5], [Reference Khanduja and Kumar12, Theorem 1.1]), we can write ![]() $G(x) = H_1(x)\cdots H_k(x)$, where the ϕ-Newton polygon of
$G(x) = H_1(x)\cdots H_k(x)$, where the ϕ-Newton polygon of ![]() $H_i(x) \in \mathbb{Z}_p[x]$ has a single edge, say
$H_i(x) \in \mathbb{Z}_p[x]$ has a single edge, say ![]() $S_i'$ which is a translate of Si. Let
$S_i'$ which is a translate of Si. Let ![]() $T_i(Y)$ belonging to
$T_i(Y)$ belonging to ![]() ${\mathbb{F}}_{p}[\overline{\alpha}][Y]$ denote the polynomial associated to
${\mathbb{F}}_{p}[\overline{\alpha}][Y]$ denote the polynomial associated to ![]() $H_i(x)$ with respect to (
$H_i(x)$ with respect to (![]() $\phi,~S_i'$) described as in Definition 2.4. The polynomial G(x) is said to be p-regular with respect to ϕ if none of the polynomials
$\phi,~S_i'$) described as in Definition 2.4. The polynomial G(x) is said to be p-regular with respect to ϕ if none of the polynomials ![]() $T_i(Y)$ has a repeated root in the algebraic closure of
$T_i(Y)$ has a repeated root in the algebraic closure of ![]() $\mathbb{F}_p$,
$\mathbb{F}_p$, ![]() $1\leq i\leq k$. In general, if g(x) belonging to
$1\leq i\leq k$. In general, if g(x) belonging to ![]() $\mathbb{Z}_p[x]$ is a monic polynomial and
$\mathbb{Z}_p[x]$ is a monic polynomial and ![]() $\overline{g}(x) = \overline{\phi}_{1}(x)^{e_1}\cdots\overline{\phi}_r{(x)}^{e_r}$ is its factorization modulo p into irreducible polynomials with each
$\overline{g}(x) = \overline{\phi}_{1}(x)^{e_1}\cdots\overline{\phi}_r{(x)}^{e_r}$ is its factorization modulo p into irreducible polynomials with each ![]() $\phi_i(x)$ belonging to
$\phi_i(x)$ belonging to ![]() $\mathbb{Z}[x]$ monic and
$\mathbb{Z}[x]$ monic and ![]() $e_i \gt 0$, then by Hensel’s Lemma [Reference Borevich and Shafarevich4, Chapter 4, Section 3], there exist monic polynomials
$e_i \gt 0$, then by Hensel’s Lemma [Reference Borevich and Shafarevich4, Chapter 4, Section 3], there exist monic polynomials ![]() $G_1(x), \dots, G_r(x)$ belonging to
$G_1(x), \dots, G_r(x)$ belonging to ![]() $\mathbb{Z}_p[x]$ such that
$\mathbb{Z}_p[x]$ such that ![]() $g(x) = G_1(x)\cdots G_r(x)$ and
$g(x) = G_1(x)\cdots G_r(x)$ and ![]() $\overline{G}_i(x) = \overline{\phi}_i(x)^{e_i}$ for each i. The polynomial g(x) is said to be p-regular with respect to
$\overline{G}_i(x) = \overline{\phi}_i(x)^{e_i}$ for each i. The polynomial g(x) is said to be p-regular with respect to ![]() $\phi_1, \dots, \phi_r$ if each
$\phi_1, \dots, \phi_r$ if each ![]() $G_i(x)$ is p-regular with respect to ϕi.
$G_i(x)$ is p-regular with respect to ϕi.
We give below a simple example of a p-regular polynomial with respect to any monic polynomial ![]() $\phi(x)\in \mathbb{Z}[x]$ which is irreducible modulo a given prime p.
$\phi(x)\in \mathbb{Z}[x]$ which is irreducible modulo a given prime p.
Example 2.7. If ![]() $p,\phi(x)$ are as above and
$p,\phi(x)$ are as above and ![]() $G(x) \ne \phi(x)$ belonging to
$G(x) \ne \phi(x)$ belonging to ![]() $\mathbb{Z}_p[x]$ is a monic polynomial with
$\mathbb{Z}_p[x]$ is a monic polynomial with ![]() $\overline{G}(x)=\overline{\phi}(x)$, then the ϕ-Newton polygon of G(x) with respect to p is a line segment S joining the point
$\overline{G}(x)=\overline{\phi}(x)$, then the ϕ-Newton polygon of G(x) with respect to p is a line segment S joining the point ![]() $(0,0)$ with
$(0,0)$ with ![]() $(1,c)$ for some c > 0. Consequently, the polynomial associated to G(x) with respect to
$(1,c)$ for some c > 0. Consequently, the polynomial associated to G(x) with respect to ![]() $(\phi,S)$ is linear and
$(\phi,S)$ is linear and ![]() $i_{\phi}(G)=0$. In particular, G(x) is p-regular with respect to ϕ.
$i_{\phi}(G)=0$. In particular, G(x) is p-regular with respect to ϕ.
We now state a celebrated result to be used in the sequel known as the Theorem of Index of Ore (cf. [Reference Khanduja and Kumar13, Theorem 1.4], [Reference Ore18]).
Theorem 2.E.
Let ![]() $L=\mathbb{Q}(\xi),g(x), p$ and
$L=\mathbb{Q}(\xi),g(x), p$ and ![]() $\phi_1(x),\dots ,\phi_r(x)$ be as in Theorem 2.D. If g(x) is p-regular with respect to
$\phi_1(x),\dots ,\phi_r(x)$ be as in Theorem 2.D. If g(x) is p-regular with respect to ![]() $\phi_1,\dots ,\phi_r$, then
$\phi_1,\dots ,\phi_r$, then  $v_p({\rm ind}\ \xi)=\sum\limits_{j=1}^{r}i_{\phi_j}(g).$
$v_p({\rm ind}\ \xi)=\sum\limits_{j=1}^{r}i_{\phi_j}(g).$
Keeping in mind Example 2.7, the following corollary is an immediate consequence of Theorem 2.E.
Corollary 2.8. Let ![]() $L=\mathbb{Q}(\xi),g(x),p$,
$L=\mathbb{Q}(\xi),g(x),p$, ![]() $\phi_1(x),\dots ,\phi_r(x)$ and
$\phi_1(x),\dots ,\phi_r(x)$ and ![]() $e_1, \dots, e_r$ be as in Theorem 2.D. If
$e_1, \dots, e_r$ be as in Theorem 2.D. If ![]() $e_i=1$ for each i > 1 and g(x) is p-regular with respect to ϕ 1, then
$e_i=1$ for each i > 1 and g(x) is p-regular with respect to ϕ 1, then ![]() $v_p({\rm ind}\ \xi)=i_{\phi_1}(g)$.
$v_p({\rm ind}\ \xi)=i_{\phi_1}(g)$.
Let ![]() $g(x),p,\phi_1(x),\dots,\phi_r(x)$ be as in Theorem 2.D. Then by Hensel’s Lemma, we can write
$g(x),p,\phi_1(x),\dots,\phi_r(x)$ be as in Theorem 2.D. Then by Hensel’s Lemma, we can write ![]() $g(x)=G_1(x)\cdots G_r(x)$ where
$g(x)=G_1(x)\cdots G_r(x)$ where ![]() $G_i(x)\in \mathbb{Z}_p[x]$ is a monic polynomial with
$G_i(x)\in \mathbb{Z}_p[x]$ is a monic polynomial with ![]() $\overline{G}_i(x)=\overline{\phi_i}(x)^{e_i}$. If S is an edge of the ϕi-Newton polygon of
$\overline{G}_i(x)=\overline{\phi_i}(x)^{e_i}$. If S is an edge of the ϕi-Newton polygon of ![]() $G_i(x)$, then for convenience, the polynomial associated to
$G_i(x)$, then for convenience, the polynomial associated to ![]() $G_i(x)$ with respect to
$G_i(x)$ with respect to ![]() $(\phi_i,~S)$ will be referred to as the polynomial associated to g(x) with respect to
$(\phi_i,~S)$ will be referred to as the polynomial associated to g(x) with respect to ![]() $(\phi_i,~S')$ where Sʹ is the edge of the ϕi-Newton polygon of g(x) which is a translate of S, because the ϕi-Newton polygon of g(x) can be obtained from the ϕi-Newton polygon of
$(\phi_i,~S')$ where Sʹ is the edge of the ϕi-Newton polygon of g(x) which is a translate of S, because the ϕi-Newton polygon of g(x) can be obtained from the ϕi-Newton polygon of ![]() $G_i(x)$ by giving a horizontal translation in view of the following simple lemma proved in [Reference Cohen, Movahhedi and Salinier5, Proposition 1.2, Theorem 3.2] and [Reference Khanduja and Kumar12, Corollary 2.5].
$G_i(x)$ by giving a horizontal translation in view of the following simple lemma proved in [Reference Cohen, Movahhedi and Salinier5, Proposition 1.2, Theorem 3.2] and [Reference Khanduja and Kumar12, Corollary 2.5].
Lemma 2.F
Let ![]() $\phi(x)\in \mathbb{Z}[x]$ be a monic polynomial which is irreducible modulo a given prime p and f(x), g(x) belonging to
$\phi(x)\in \mathbb{Z}[x]$ be a monic polynomial which is irreducible modulo a given prime p and f(x), g(x) belonging to ![]() $\mathbb{Z}_p[x]$ be two monic polynomials not divisible by
$\mathbb{Z}_p[x]$ be two monic polynomials not divisible by ![]() $\phi(x)$. If
$\phi(x)$. If ![]() $\overline{\phi}(x)$ does not divide
$\overline{\phi}(x)$ does not divide ![]() $\overline{g}(x)$, then the ϕ-Newton polygon of g(x) is either a point or a horizontal line segment and the ϕ-Newton polygon of
$\overline{g}(x)$, then the ϕ-Newton polygon of g(x) is either a point or a horizontal line segment and the ϕ-Newton polygon of ![]() $f(x)g(x)$ is obtained by adjoining to the ϕ-Newton polygon of g(x) a translate of the ϕ-Newton polygon of f(x).
$f(x)g(x)$ is obtained by adjoining to the ϕ-Newton polygon of g(x) a translate of the ϕ-Newton polygon of f(x).
3. Proof of Theorem 1.1
The proof of Theorem 1.1 is divided in four steps.
Step I. In this step, we prove that for any prime p less than or equal to n, x is the only repeated factor of ![]() $f_n(x)$ modulo p. In view of Lemma 2.A and a well-known result [Reference Khanduja11, Corollary 2.16], we have
$f_n(x)$ modulo p. In view of Lemma 2.A and a well-known result [Reference Khanduja11, Corollary 2.16], we have
 \begin{equation}
(-1)^{\frac{n(n-1)}{2}} (n!)^{n}=discr (f_n)= ({\rm ind}\ \theta)^2 d_K.
\end{equation}
\begin{equation}
(-1)^{\frac{n(n-1)}{2}} (n!)^{n}=discr (f_n)= ({\rm ind}\ \theta)^2 d_K.
\end{equation} So if a prime divides ![]() ${\rm ind}\ \theta$ or dK, then it divides
${\rm ind}\ \theta$ or dK, then it divides ![]() $n!$. Let p be a prime dividing
$n!$. Let p be a prime dividing ![]() $n!$. Let k be the smallest non-negative integer not exceeding n − 2 such that p divides n − k. Then
$n!$. Let k be the smallest non-negative integer not exceeding n − 2 such that p divides n − k. Then
 \begin{equation*}
f_n(x)\equiv x^{n-k} \left( x^{k} + \frac{n!}{(n-1)!}x^{k-1}+\cdots + \frac{n!}{(n-k)!}\right) \pmod p.
\end{equation*}
\begin{equation*}
f_n(x)\equiv x^{n-k} \left( x^{k} + \frac{n!}{(n-1)!}x^{k-1}+\cdots + \frac{n!}{(n-k)!}\right) \pmod p.
\end{equation*} Denote the polynomial  $ x^{k} +\frac{n!}{(n-1)!}x^{k-1}+\cdots + \frac{n!}{(n-k)!}$ by h(x). Note that h(x) is not divisible by x modulo p in view of the choice of k and
$ x^{k} +\frac{n!}{(n-1)!}x^{k-1}+\cdots + \frac{n!}{(n-k)!}$ by h(x). Note that h(x) is not divisible by x modulo p in view of the choice of k and ![]() $h(x)\equiv x^{k} +h{'}(x) \pmod p$. So h(x) and
$h(x)\equiv x^{k} +h{'}(x) \pmod p$. So h(x) and ![]() $h{'}(x)$ are coprime modulo p, i.e., h(x) has no repeated factor modulo p. Consequently x is the only repeated factor of
$h{'}(x)$ are coprime modulo p, i.e., h(x) has no repeated factor modulo p. Consequently x is the only repeated factor of ![]() $f_n(x)$ modulo p.
$f_n(x)$ modulo p.
Step II. In this step, we prove that ![]() $f_n(x)$ is p-regular with respect to
$f_n(x)$ is p-regular with respect to ![]() $\phi(x)=x$ for each prime p dividing
$\phi(x)=x$ for each prime p dividing ![]() $n!$. Let p be such a prime. Keeping in mind that x is the only repeated factor of
$n!$. Let p be such a prime. Keeping in mind that x is the only repeated factor of ![]() $f_n(x)$ modulo p in view of Step I, it would follow from Corollary 2.8 that
$f_n(x)$ modulo p in view of Step I, it would follow from Corollary 2.8 that ![]() $v_p(\text{ind} \ \theta)=i_{\phi}(f_n)$ where
$v_p(\text{ind} \ \theta)=i_{\phi}(f_n)$ where ![]() $\phi(x)=x$, i.e.,
$\phi(x)=x$, i.e.,
where N is the number of points with positive integer coordinates lying on or below the Newton polygon of ![]() $f_{n}(x)$ with respect to p away from the vertical line passing through the last vertex of this polygon.
$f_{n}(x)$ with respect to p away from the vertical line passing through the last vertex of this polygon.
By definition, the Newton polygon of ![]() $f_n(x)$ with respect to p is the polygonal path formed by the lower edges along the convex hull of points of the set
$f_n(x)$ with respect to p is the polygonal path formed by the lower edges along the convex hull of points of the set ![]() $\mathcal{P}$ defined by
$\mathcal{P}$ defined by
Recall that
where ![]() $0\leq m_1 \lt m_2 \lt \cdots \lt m_s$ and
$0\leq m_1 \lt m_2 \lt \cdots \lt m_s$ and ![]() $0 \lt c_i \lt p$ for each i. Set
$0 \lt c_i \lt p$ for each i. Set ![]() $z_0=0$ and
$z_0=0$ and
As in [Reference Coleman6], making use of Lemma 2.B, it can be easily shown that the Newton polygon of ![]() $f_n(x)$ with respect to p consists of s edges; the ith edge from left to right is the line segment joining the points:
$f_n(x)$ with respect to p consists of s edges; the ith edge from left to right is the line segment joining the points:
Therefore using Lemma 2.B, we see that the slope λi of the ith edge of the Newton polygon of ![]() $f_n(x)$ with respect to p is given by:
$f_n(x)$ with respect to p is given by:
 \begin{align*}
\lambda_i
&=\frac{-v_p((n-z_{i})!)+v_p((n-z_{i-1})!)}{z_i-z_{i-1}}\\
&=\frac{z_{i}+(c_{i+1}+\cdots+c_{s})-z_{i-1}-(c_i+\cdots+c_{s})}{(z_i-z_{i-1})(p-1)}.
\end{align*}
\begin{align*}
\lambda_i
&=\frac{-v_p((n-z_{i})!)+v_p((n-z_{i-1})!)}{z_i-z_{i-1}}\\
&=\frac{z_{i}+(c_{i+1}+\cdots+c_{s})-z_{i-1}-(c_i+\cdots+c_{s})}{(z_i-z_{i-1})(p-1)}.
\end{align*}So
 \begin{align*}
\lambda_i=\frac{c_{i}p^{m_{i}}-c_{i}}{c_{i}p^{m_{i}}(p-1)}=\frac{p^{m_{i}}-1}{p^{m_{i}}(p-1)}.
\end{align*}
\begin{align*}
\lambda_i=\frac{c_{i}p^{m_{i}}-c_{i}}{c_{i}p^{m_{i}}(p-1)}=\frac{p^{m_{i}}-1}{p^{m_{i}}(p-1)}.
\end{align*} Note that ![]() $f_n(x)$ has an edge with slope zero if and only if
$f_n(x)$ has an edge with slope zero if and only if ![]() $m_1=0$, which happens only when k > 0 where k is as in Step I. In view of Hensel’s Lemma and the Theorem of product by Ore (cf. [Reference Cohen, Movahhedi and Salinier5, Theorem 1.5], [Reference Khanduja and Kumar12, Theorem 1.1]), we can write
$m_1=0$, which happens only when k > 0 where k is as in Step I. In view of Hensel’s Lemma and the Theorem of product by Ore (cf. [Reference Cohen, Movahhedi and Salinier5, Theorem 1.5], [Reference Khanduja and Kumar12, Theorem 1.1]), we can write ![]() $f_n(x)= G_1(x)\cdots G_{s}(x)$ where
$f_n(x)= G_1(x)\cdots G_{s}(x)$ where ![]() $G_i(x)\in \mathbb{Z}_p[x]$ has degree
$G_i(x)\in \mathbb{Z}_p[x]$ has degree ![]() $z_i-z_{i-1}=c_ip^{m_i}$ and the Newton polygon of
$z_i-z_{i-1}=c_ip^{m_i}$ and the Newton polygon of ![]() $G_i(x)$ with respect to p consists of only one edge Si (say) having slope λi. When
$G_i(x)$ with respect to p consists of only one edge Si (say) having slope λi. When ![]() $\lambda_i \gt 0$, let
$\lambda_i \gt 0$, let ![]() $T_i(Y)$ belonging to
$T_i(Y)$ belonging to ![]() ${\mathbb{F}}_{p}[Y]$ denote the polynomial associated to
${\mathbb{F}}_{p}[Y]$ denote the polynomial associated to ![]() $G_i(x)$ with respect to (
$G_i(x)$ with respect to (![]() $\phi,~S_i$) as described in Definition 2.6, where
$\phi,~S_i$) as described in Definition 2.6, where ![]() $\phi(x)=x$. Note that the degree of
$\phi(x)=x$. Note that the degree of ![]() $T_i(Y)$ is
$T_i(Y)$ is ![]() $c_i\leq p-1$; consequently
$c_i\leq p-1$; consequently ![]() $T_i(Y)$ is a separable polynomial. This proves that
$T_i(Y)$ is a separable polynomial. This proves that ![]() $f_n(x)$ is p-regular with respect to
$f_n(x)$ is p-regular with respect to ![]() $\phi(x)=x$.
$\phi(x)=x$.
Step III. In this step, we prove that
 \begin{equation}
N=\frac 12
\sum\limits_{i=1}^{s}[c_id_i\left(c_ip^{m_i}+2c_{i+1}p^{m_{i+1}}+\cdots+2c_sp^{m_s}-p\right) ],
\end{equation}
\begin{equation}
N=\frac 12
\sum\limits_{i=1}^{s}[c_id_i\left(c_ip^{m_i}+2c_{i+1}p^{m_{i+1}}+\cdots+2c_sp^{m_s}-p\right) ],
\end{equation}where N is as in (5). This will prove (1) at once.
Set ![]() $t_i=v_p(n!/(n-z_i)!)$ for
$t_i=v_p(n!/(n-z_i)!)$ for ![]() $0\leq i \leq s$. Using Lemma 2.B, it can be easily seen that
$0\leq i \leq s$. Using Lemma 2.B, it can be easily seen that ![]() $v_p(n!/(n-z_i)!)=v_p(z_i!)$ for
$v_p(n!/(n-z_i)!)=v_p(z_i!)$ for ![]() $0\leq i \leq s$. So
$0\leq i \leq s$. So ![]() $t_0=0$ and
$t_0=0$ and
As pointed out in Step II, the Newton polygon of ![]() $f_{n}(x)$ with respect to p consists of s edges; the ith edge from left to right is the segment joining the points
$f_{n}(x)$ with respect to p consists of s edges; the ith edge from left to right is the segment joining the points ![]() $(z_{i-1}, t_{i-1}),\ (z_i, t_i)$ and N is the number of points with positive integer coordinates lying on or below this Newton polygon which do not lie on the line
$(z_{i-1}, t_{i-1}),\ (z_i, t_i)$ and N is the number of points with positive integer coordinates lying on or below this Newton polygon which do not lie on the line ![]() $x=z_s$. We now count these points.
$x=z_s$. We now count these points.
For ![]() $1\leq i \leq s$, the number of points with positive integer coordinates lying on or in the triangle joining the points
$1\leq i \leq s$, the number of points with positive integer coordinates lying on or in the triangle joining the points ![]() $(z_{i-1},t_{i-1})$,
$(z_{i-1},t_{i-1})$, ![]() $(z_i,t_{i-1})$,
$(z_i,t_{i-1})$, ![]() $(z_i,t_i)$ away from its vertical side is same as number of such points in the case of the triangle joining
$(z_i,t_i)$ away from its vertical side is same as number of such points in the case of the triangle joining ![]() $(0,0)$,
$(0,0)$, ![]() $(z_i-z_{i-1}, 0)$,
$(z_i-z_{i-1}, 0)$, ![]() $(z_i-z_{i-1}, t_i-t_{i-1})$. It is immediate from (6) and (8) that
$(z_i-z_{i-1}, t_i-t_{i-1})$. It is immediate from (6) and (8) that ![]() $z_i-z_{i-1}=c_ip^{m_i}$ and
$z_i-z_{i-1}=c_ip^{m_i}$ and ![]() $t_i-t_{i-1}=c_id_i$. In view of Lemma 2.C, this number is given by:
$t_i-t_{i-1}=c_id_i$. In view of Lemma 2.C, this number is given by:
 \begin{align*}
\frac 12[(c_ip^{m_i}-1)\left(c_id_i-1\right)+c_i-1] &= \frac 12[c_i^2d_ip^{m_i}-c_id_i-c_ip^{m_i}+c_i]
=\frac 12 c_id_i [c_ip^{m_i}-p].
\end{align*}
\begin{align*}
\frac 12[(c_ip^{m_i}-1)\left(c_id_i-1\right)+c_i-1] &= \frac 12[c_i^2d_ip^{m_i}-c_id_i-c_ip^{m_i}+c_i]
=\frac 12 c_id_i [c_ip^{m_i}-p].
\end{align*} For ![]() $2\leq i \leq s$, the number of points with positive integer coordinates lying in or on the rectangle joining the points
$2\leq i \leq s$, the number of points with positive integer coordinates lying in or on the rectangle joining the points ![]() $(z_{i-1},0)$,
$(z_{i-1},0)$, ![]() $(z_i,0)$,
$(z_i,0)$, ![]() $(z_i, t_{i-1})$ and
$(z_i, t_{i-1})$ and ![]() $(z_{i-1}, t_{i-1})$ which do not lie on the line
$(z_{i-1}, t_{i-1})$ which do not lie on the line ![]() $x=z_i$ is
$x=z_i$ is ![]() $(z_i-z_{i-1})t_{i-1}=c_ip^{m_i}(c_1d_1+\cdots +c_{i-1}d_{i-1})$ by virtue of (6) and (8). Therefore
$(z_i-z_{i-1})t_{i-1}=c_ip^{m_i}(c_1d_1+\cdots +c_{i-1}d_{i-1})$ by virtue of (6) and (8). Therefore
 \begin{align*}
\begin{split}
N&= \frac 12 \sum\limits_{i=1}^{s} c_id_i[c_ip^{m_i}-p]+ \sum\limits_{i=2}^{s} [c_ip^{m_i}(c_1d_1+\cdots +c_{i-1}d_{i-1})]\\
&= \frac 12 \sum\limits_{i=1}^{s} c_id_i[c_ip^{m_i}-p]+
\sum\limits_{i=1}^{s}[c_id_i\left(c_{i+1}p^{m_{i+1}}+\cdots+c_sp^{m_s}\right)]\\
&=\frac 12
\sum\limits_{i=1}^{s}[c_id_i\left(c_ip^{m_i}+2c_{i+1}p^{m_{i+1}}+\cdots+2c_sp^{m_s} -p\right)].
\end{split}
\end{align*}
\begin{align*}
\begin{split}
N&= \frac 12 \sum\limits_{i=1}^{s} c_id_i[c_ip^{m_i}-p]+ \sum\limits_{i=2}^{s} [c_ip^{m_i}(c_1d_1+\cdots +c_{i-1}d_{i-1})]\\
&= \frac 12 \sum\limits_{i=1}^{s} c_id_i[c_ip^{m_i}-p]+
\sum\limits_{i=1}^{s}[c_id_i\left(c_{i+1}p^{m_{i+1}}+\cdots+c_sp^{m_s}\right)]\\
&=\frac 12
\sum\limits_{i=1}^{s}[c_id_i\left(c_ip^{m_i}+2c_{i+1}p^{m_{i+1}}+\cdots+2c_sp^{m_s} -p\right)].
\end{split}
\end{align*}This proves (7) and hence (1) is proved.
Step IV. In this step, we prove (2). It is immediate from (4) that ![]() $v_p(d_K)=nv_p(n!)-2v_p({\rm ind}\ \theta)$. Using Lemma 2.B, we see that
$v_p(d_K)=nv_p(n!)-2v_p({\rm ind}\ \theta)$. Using Lemma 2.B, we see that
 \begin{align}
nv_p(n!)=(c_1p^{m_1}+\cdots+c_sp^{m_s})\left(c_1d_1+\cdots+c_sd_s\right)=\sum\limits_{i=1}^{s}[c_id_i(c_1p^{m_1}+\cdots+c_sp^{m_s})].
\end{align}
\begin{align}
nv_p(n!)=(c_1p^{m_1}+\cdots+c_sp^{m_s})\left(c_1d_1+\cdots+c_sd_s\right)=\sum\limits_{i=1}^{s}[c_id_i(c_1p^{m_1}+\cdots+c_sp^{m_s})].
\end{align}It is immediate from (1) and (9) that
 \begin{align}
v_p(d_K)&=nv_p(n!)-2v_p({\rm ind}\ \theta)\nonumber\\
&=\sum\limits_{i=1}^{s}[c_id_i(c_1p^{m_1}+\cdots+c_sp^{m_s})]
-\sum\limits_{i=1}^{s} [c_id_i\left(c_ip^{m_i}+2c_{i+1}p^{m_{i+1}}+\cdots+2c_sp^{m_s}\right)]\nonumber\\
& \qquad +p\sum\limits_{i=1}^{s}c_id_i\nonumber\\
&=\sum\limits_{i=1}^{s} [c_id_i(c_1p^{m_1}+\cdots+c_{i-1}p^{m_{i-1}}-c_{i+1}p^{m_{i+1}}-\cdots-c_sp^{m_s})]+p\sum\limits_{i=1}^{s} c_id_i.
\end{align}
\begin{align}
v_p(d_K)&=nv_p(n!)-2v_p({\rm ind}\ \theta)\nonumber\\
&=\sum\limits_{i=1}^{s}[c_id_i(c_1p^{m_1}+\cdots+c_sp^{m_s})]
-\sum\limits_{i=1}^{s} [c_id_i\left(c_ip^{m_i}+2c_{i+1}p^{m_{i+1}}+\cdots+2c_sp^{m_s}\right)]\nonumber\\
& \qquad +p\sum\limits_{i=1}^{s}c_id_i\nonumber\\
&=\sum\limits_{i=1}^{s} [c_id_i(c_1p^{m_1}+\cdots+c_{i-1}p^{m_{i-1}}-c_{i+1}p^{m_{i+1}}-\cdots-c_sp^{m_s})]+p\sum\limits_{i=1}^{s} c_id_i.
\end{align} Keeping in mind that  $d_i=\frac{p^{m_i}-1}{p-1}$, it can be easily seen that:
$d_i=\frac{p^{m_i}-1}{p-1}$, it can be easily seen that:  $d_jp^{m_i}-d_ip^{m_j}=\frac{p^{m_j}-p^{m_i}}{p-1}$ for
$d_jp^{m_i}-d_ip^{m_j}=\frac{p^{m_j}-p^{m_i}}{p-1}$ for ![]() $1\leq i \lt j\leq s$. Using this equality, the first summand in (10) can be rewritten as:
$1\leq i \lt j\leq s$. Using this equality, the first summand in (10) can be rewritten as:
 \begin{align*}
& \sum\limits_{1\leq j \lt i \leq s} (c_ic_jd_ip^{m_j})-\sum\limits_{1\leq i \lt j \leq s} (c_ic_jd_ip^{m_j})
=\sum\limits_{1\leq i \lt j \leq s} [c_ic_j(d_jp^{m_i}-d_ip^{m_j})]\\
& \qquad =\sum\limits_{1\leqslant i \lt j\leqslant s} \frac{c_ic_j(p^{m_j}-p^{m_i})}{p-1}.
\end{align*}
\begin{align*}
& \sum\limits_{1\leq j \lt i \leq s} (c_ic_jd_ip^{m_j})-\sum\limits_{1\leq i \lt j \leq s} (c_ic_jd_ip^{m_j})
=\sum\limits_{1\leq i \lt j \leq s} [c_ic_j(d_jp^{m_i}-d_ip^{m_j})]\\
& \qquad =\sum\limits_{1\leqslant i \lt j\leqslant s} \frac{c_ic_j(p^{m_j}-p^{m_i})}{p-1}.
\end{align*}4. Proof of Corollaries 1.2, 1.3
Proof of Corollary 1.2.
Let p be a prime number. In view of (1), ![]() $v_p({\rm ind}\ \theta)=0$ if and only if the p-adic expansion of n is of the type
$v_p({\rm ind}\ \theta)=0$ if and only if the p-adic expansion of n is of the type ![]() $n=c_1$ or n = p or
$n=c_1$ or n = p or ![]() $n=c_1+p$ with
$n=c_1+p$ with ![]() $0 \lt c_1 \lt p$, which is equivalent to saying that
$0 \lt c_1 \lt p$, which is equivalent to saying that ![]() $n \lt 2p$. This proves the first assertion of the corollary. The second assertion follows immediately from the first.
$n \lt 2p$. This proves the first assertion of the corollary. The second assertion follows immediately from the first.
5. Proof of Theorem 1.4
The following proposition to be used in the sequel is proved as Proposition 3.A in [Reference Kaur and Khanduja10].
Proposition 5.A.
Let ![]() $L=\mathbb{Q}(\xi)$ be an algebraic number field of degree n with ξ an algebraic integer and let p be a prime number. Let
$L=\mathbb{Q}(\xi)$ be an algebraic number field of degree n with ξ an algebraic integer and let p be a prime number. Let ![]() $\alpha_1,\alpha_2,\dots ,\alpha_{n-1}$ be p-integral elements of L of the type
$\alpha_1,\alpha_2,\dots ,\alpha_{n-1}$ be p-integral elements of L of the type  $\alpha_i=\frac{c_{i0}+c_{i1}\xi+\cdots +c_{i(i-1)}\xi^{i-1}+\xi^i}{p^{k_i}}$ where
$\alpha_i=\frac{c_{i0}+c_{i1}\xi+\cdots +c_{i(i-1)}\xi^{i-1}+\xi^i}{p^{k_i}}$ where ![]() $c_{ij},~k_i$ are in
$c_{ij},~k_i$ are in ![]() $\mathbb{Z}$ with
$\mathbb{Z}$ with ![]() $0\leq k_i\leq k_{i+1}$ for
$0\leq k_i\leq k_{i+1}$ for ![]() $1\leq i\leq n-2$. Then
$1\leq i\leq n-2$. Then ![]() $\{1,\alpha_1,\dots ,\alpha_{n-1}\}$ is a p-integral basis of L if and only if
$\{1,\alpha_1,\dots ,\alpha_{n-1}\}$ is a p-integral basis of L if and only if  $v_p({\rm ind}~\xi)=\displaystyle\sum_{i=1}^{n-1}k_i$.
$v_p({\rm ind}~\xi)=\displaystyle\sum_{i=1}^{n-1}k_i$.
Recall that an algebraic number η is integral over the localisation ![]() $\mathbb{Z}_{(p)}$ of
$\mathbb{Z}_{(p)}$ of ![]() $\mathbb{Z}$ at a maximal ideal
$\mathbb{Z}$ at a maximal ideal ![]() $p\mathbb{Z}$ if and only if
$p\mathbb{Z}$ if and only if ![]() $w(\eta)\geq 0$ for all prolongations w to
$w(\eta)\geq 0$ for all prolongations w to ![]() $\mathbb{Q}(\eta)$ of the p-adic valuation of
$\mathbb{Q}(\eta)$ of the p-adic valuation of ![]() $\mathbb{Q}$ (cf. [Reference Borevich and Shafarevich4, Chapter 3, Theorem 6]). Keeping this in mind the next proposition follows immediately from Proposition 2.2 of [Reference Khanduja and Kumar13]. Its proof is omitted.
$\mathbb{Q}$ (cf. [Reference Borevich and Shafarevich4, Chapter 3, Theorem 6]). Keeping this in mind the next proposition follows immediately from Proposition 2.2 of [Reference Khanduja and Kumar13]. Its proof is omitted.
Proposition 5.B.
Let ![]() $\mathbb{Q}(\xi)$ be an algebraic number field, where ξ is a root of a monic irreducible polynomial g(x) belonging to
$\mathbb{Q}(\xi)$ be an algebraic number field, where ξ is a root of a monic irreducible polynomial g(x) belonging to ![]() $\mathbb{Z}[x]$. Let
$\mathbb{Z}[x]$. Let ![]() $\phi(x)\in\mathbb{Z}[x]$ be a monic polynomial different from g(x) which divides g(x) modulo a given prime p and is irreducible modulo p. Let
$\phi(x)\in\mathbb{Z}[x]$ be a monic polynomial different from g(x) which divides g(x) modulo a given prime p and is irreducible modulo p. Let  $g(x)=\sum\limits_{i=0}^{d} g_i(x)\phi(x)^i$ be the ϕ-expansion of g(x) with
$g(x)=\sum\limits_{i=0}^{d} g_i(x)\phi(x)^i$ be the ϕ-expansion of g(x) with ![]() $g_d(x)\ne0$. Let
$g_d(x)\ne0$. Let ![]() $q_j(x)$ denote the quotient obtained on dividing g(x) by
$q_j(x)$ denote the quotient obtained on dividing g(x) by ![]() $\phi(x)^{j}$,
$\phi(x)^{j}$, ![]() $1\leq j\leq d$. If
$1\leq j\leq d$. If ![]() $y_{d-j}$ stands for the ordinate of the point with abscissa d − j on the ϕ-Newton polygon of g(x) with respect to p, then
$y_{d-j}$ stands for the ordinate of the point with abscissa d − j on the ϕ-Newton polygon of g(x) with respect to p, then  $q_j(\xi)/p^{\lfloor y_{d-j}\rfloor }$ is integral over
$q_j(\xi)/p^{\lfloor y_{d-j}\rfloor }$ is integral over ![]() $\mathbb{Z}_{(p)}$.
$\mathbb{Z}_{(p)}$.
The result stated below is an immediate consequence of Corollary 2.8 and Propositions 5.A, 5.B.
Proposition 5.1. Let ![]() $L=\mathbb{Q}(\xi)$ be an algebraic number field with ξ satisfying a monic irreducible polynomial
$L=\mathbb{Q}(\xi)$ be an algebraic number field with ξ satisfying a monic irreducible polynomial ![]() $g(x) \in \mathbb{Z}[x]$ of degree n and let p be a prime number. Let
$g(x) \in \mathbb{Z}[x]$ of degree n and let p be a prime number. Let ![]() $ \overline{\phi}_{1}(x)^{e_1}\cdots\overline{\phi}_r{(x)}^{e_r}$ be the factorization of
$ \overline{\phi}_{1}(x)^{e_1}\cdots\overline{\phi}_r{(x)}^{e_r}$ be the factorization of ![]() ${g}(x)$ modulo p into a product of powers of distinct irreducible polynomials over
${g}(x)$ modulo p into a product of powers of distinct irreducible polynomials over ![]() $\mathbb{F}_p$, where each
$\mathbb{F}_p$, where each ![]() $\phi_i(x) \neq g(x)$ belonging to
$\phi_i(x) \neq g(x)$ belonging to ![]() $\mathbb{Z}[x]$ is monic. Assume that
$\mathbb{Z}[x]$ is monic. Assume that ![]() $\phi_1(x)=x$,
$\phi_1(x)=x$, ![]() $e_i=1$ for each i > 1 and g(x) is p-regular with respect to ϕ 1. Let
$e_i=1$ for each i > 1 and g(x) is p-regular with respect to ϕ 1. Let ![]() $q_j(x)$ denote the quotient obtained on dividing g(x) by x j,
$q_j(x)$ denote the quotient obtained on dividing g(x) by x j, ![]() $1\leq j\leq n-1$. If
$1\leq j\leq n-1$. If ![]() $y_{n-j}$ stands for the ordinate of the point with abscissa n − j on the ϕ 1-Newton polygon of g(x) with respect to p, then
$y_{n-j}$ stands for the ordinate of the point with abscissa n − j on the ϕ 1-Newton polygon of g(x) with respect to p, then ![]() $\{1,q_1(\xi)/p^{\lfloor y_{n-1}\rfloor}, \dots, q_{n-1}(\xi)/p^{\lfloor y_{1} \rfloor}\}$ is a p-integral basis of L.
$\{1,q_1(\xi)/p^{\lfloor y_{n-1}\rfloor}, \dots, q_{n-1}(\xi)/p^{\lfloor y_{1} \rfloor}\}$ is a p-integral basis of L.
Proof of Theorem 1.4.
In view of Steps I and II of the proof of Theorem 1.1 given in ![]() $\S$ 3, we see that
$\S$ 3, we see that ![]() $f_n(x)$ satisfies the hypothesis of Proposition 5.1. Therefore, Theorem 1.4 follows immediately from Proposition 5.1, because with notations as in Proposition 5.1, we have
$f_n(x)$ satisfies the hypothesis of Proposition 5.1. Therefore, Theorem 1.4 follows immediately from Proposition 5.1, because with notations as in Proposition 5.1, we have  $q_{n-j}(x)=x^{j}+\frac{n!}{(n-1)!}x^{j-1}+\cdots+\frac{n!}{(n-j)!}=u_j(x)$ for
$q_{n-j}(x)=x^{j}+\frac{n!}{(n-1)!}x^{j-1}+\cdots+\frac{n!}{(n-j)!}=u_j(x)$ for ![]() $1\leq j \leq n-1$.
$1\leq j \leq n-1$.
Example 5.2. Let ![]() $K=\mathbb{Q}(\theta)$ where θ is a root of the polynomial,
$K=\mathbb{Q}(\theta)$ where θ is a root of the polynomial,
 \begin{equation*}
f_6(x)=x^6+ \frac{6!}{5!}x^5+\frac{6!}{4!}x^4 +\frac{6!}{3!}x^3 +\frac{6!}{2!}x^2 +\frac{6!}{1!}x +6!.
\end{equation*}
\begin{equation*}
f_6(x)=x^6+ \frac{6!}{5!}x^5+\frac{6!}{4!}x^4 +\frac{6!}{3!}x^3 +\frac{6!}{2!}x^2 +\frac{6!}{1!}x +6!.
\end{equation*} Then by (2), ![]() $v_2(d_K)=10$,
$v_2(d_K)=10$, ![]() $v_3(d_K)=6$ and
$v_3(d_K)=6$ and ![]() $v_5(d_K)=6$. So
$v_5(d_K)=6$. So ![]() $d_K=-2^{10}3^65^6$ in view of Lemma 2.A. By virtue of Corollary 1.2, we see that
$d_K=-2^{10}3^65^6$ in view of Lemma 2.A. By virtue of Corollary 1.2, we see that ![]() $v_p({\rm ind}\ \theta) \gt 0$ only when p = 2 or 3. For these two primes, we first find p-integral bases. Keeping the notations
$v_p({\rm ind}\ \theta) \gt 0$ only when p = 2 or 3. For these two primes, we first find p-integral bases. Keeping the notations ![]() $u_j(x)$ and yj of Theorem 1.4, we have
$u_j(x)$ and yj of Theorem 1.4, we have
 \begin{equation*}
u_j(x)=x^{j}+\frac{6!}{5!}x^{j-1}+\cdots+\frac{6!}{(6-j)!},\quad 1\leq j \leq 5.
\end{equation*}
\begin{equation*}
u_j(x)=x^{j}+\frac{6!}{5!}x^{j-1}+\cdots+\frac{6!}{(6-j)!},\quad 1\leq j \leq 5.
\end{equation*} The Newton polygon of ![]() $f_{6}(x)$ with respect to the prime 2 has two edges joining the points
$f_{6}(x)$ with respect to the prime 2 has two edges joining the points ![]() $(0,0)$ with
$(0,0)$ with ![]() $(2,1)$ and
$(2,1)$ and ![]() $(2,1)$ with
$(2,1)$ with ![]() $ (6,4)$. So
$ (6,4)$. So ![]() $\lfloor y_1 \rfloor=0$,
$\lfloor y_1 \rfloor=0$, ![]() $\lfloor y_2 \rfloor=\lfloor y_3 \rfloor=1$,
$\lfloor y_2 \rfloor=\lfloor y_3 \rfloor=1$, ![]() $\lfloor y_4 \rfloor=2$ and
$\lfloor y_4 \rfloor=2$ and ![]() $\lfloor y_5 \rfloor=3$. Therefore applying Theorem 1.4, we see that
$\lfloor y_5 \rfloor=3$. Therefore applying Theorem 1.4, we see that
 \begin{equation*}\left\{1,\theta, \frac{\theta^2}{2}, \frac{\theta^3}{2}, \frac{\theta^4+2\theta^3+2\theta^2}{2^2}, \frac{\theta^5+6\theta^4+6\theta^3}{2^3} \right\}\end{equation*}
\begin{equation*}\left\{1,\theta, \frac{\theta^2}{2}, \frac{\theta^3}{2}, \frac{\theta^4+2\theta^3+2\theta^2}{2^2}, \frac{\theta^5+6\theta^4+6\theta^3}{2^3} \right\}\end{equation*}is a 2-integral basis of K.
By looking at the Newton polygon of ![]() $f_{6}(x)$ with respect to the prime 3 and applying Theorem 1.4, it can be easily seen that
$f_{6}(x)$ with respect to the prime 3 and applying Theorem 1.4, it can be easily seen that  $\left\{1,\theta, \theta^2, \frac{\theta^3}{3}, \frac{\theta^4}{3}, \frac{\theta^5}{3} \right\}$ is a 3-integral basis of K.
$\left\{1,\theta, \theta^2, \frac{\theta^3}{3}, \frac{\theta^4}{3}, \frac{\theta^5}{3} \right\}$ is a 3-integral basis of K.
Therefore, using Theorem 1.A and Chinese Remainder Theorem, we see that:
 \begin{equation*}\left\{1,\theta, \frac{\theta^2}{2}, \frac{\theta^3}{6}, \frac{\theta^4+6\theta^3+6\theta^2}{12}, \frac{\theta^5+6\theta^4+6\theta^3}{24} \right\},\end{equation*}
\begin{equation*}\left\{1,\theta, \frac{\theta^2}{2}, \frac{\theta^3}{6}, \frac{\theta^4+6\theta^3+6\theta^2}{12}, \frac{\theta^5+6\theta^4+6\theta^3}{24} \right\},\end{equation*}is an integral basis of K.
Example 5.3. Let ![]() $K=\mathbb{Q}(\theta)$ where θ is a root of the polynomial:
$K=\mathbb{Q}(\theta)$ where θ is a root of the polynomial:
 \begin{equation*}
f_7(x)=x^7+
\frac{7!}{6!}x^6+ \frac{7!}{5!}x^5+\frac{7!}{4!}x^4 +\frac{7!}{3!}x^3 +\frac{7!}{2!}x^2 +\frac{7!}{1!}x +7!.
\end{equation*}
\begin{equation*}
f_7(x)=x^7+
\frac{7!}{6!}x^6+ \frac{7!}{5!}x^5+\frac{7!}{4!}x^4 +\frac{7!}{3!}x^3 +\frac{7!}{2!}x^2 +\frac{7!}{1!}x +7!.
\end{equation*} Then by (2), ![]() $v_2(d_K)=14$,
$v_2(d_K)=14$, ![]() $v_3(d_K)=8$ and
$v_3(d_K)=8$ and ![]() $v_5(d_K)=v_7(d_K)=7$. So
$v_5(d_K)=v_7(d_K)=7$. So ![]() $d_K=-2^{14}3^85^77^7$ by virtue of Lemma 2.A. In view of Corollary 1.2,
$d_K=-2^{14}3^85^77^7$ by virtue of Lemma 2.A. In view of Corollary 1.2, ![]() $v_p({\rm ind}\ \theta) \gt 0$ only when p = 2 or 3. For these two primes, we first find p-integral bases. With notations as in Theorem 1.4, we have:
$v_p({\rm ind}\ \theta) \gt 0$ only when p = 2 or 3. For these two primes, we first find p-integral bases. With notations as in Theorem 1.4, we have:
 \begin{equation*}
u_j(x)=x^{j}+\frac{7!}{6!}x^{j-1}+\cdots+\frac{7!}{(7-j)!},\quad 1\leq j \leq 6.
\end{equation*}
\begin{equation*}
u_j(x)=x^{j}+\frac{7!}{6!}x^{j-1}+\cdots+\frac{7!}{(7-j)!},\quad 1\leq j \leq 6.
\end{equation*} Keeping in mind that the Newton polygon of ![]() $f_{7}(x)$ with respect to 2 is the polygonal path joining the points
$f_{7}(x)$ with respect to 2 is the polygonal path joining the points ![]() $(0,0), (1,0), (3,1), (7,4)$ and using Theorem 1.4, it can be checked that:
$(0,0), (1,0), (3,1), (7,4)$ and using Theorem 1.4, it can be checked that:
 \begin{equation*}\left\{1,\theta, \theta^2, \frac{\theta^3+ \theta^2}{2}, \frac{\theta^4+ \theta^3}{2}, \frac{\theta^5+3\theta^4+2\theta^3+2\theta^2}{2^2},
\frac{\theta^6+7\theta^5+2\theta^4+2\theta^3}{2^3} \right\},\end{equation*}
\begin{equation*}\left\{1,\theta, \theta^2, \frac{\theta^3+ \theta^2}{2}, \frac{\theta^4+ \theta^3}{2}, \frac{\theta^5+3\theta^4+2\theta^3+2\theta^2}{2^2},
\frac{\theta^6+7\theta^5+2\theta^4+2\theta^3}{2^3} \right\},\end{equation*} is a 2-integral basis of K. By similar arguments, we can show that  $\left\{1,\theta, \theta^2, \theta^3, \frac{\theta^4+ \theta^3}{3}, \frac{\theta^5+\theta^4}{3},
\frac{\theta^6+\theta^5}{3} \right\} $ is a 3-integral basis of K. Therefore, it follows from Theorem 1.A that:
$\left\{1,\theta, \theta^2, \theta^3, \frac{\theta^4+ \theta^3}{3}, \frac{\theta^5+\theta^4}{3},
\frac{\theta^6+\theta^5}{3} \right\} $ is a 3-integral basis of K. Therefore, it follows from Theorem 1.A that:
 \begin{equation*}\left\{1,\theta, \theta^2, \frac{\theta^3+ 3\theta^2}{2}, \frac{\theta^4+ \theta^3}{6}, \frac{\theta^5+7\theta^4+6\theta^3+6\theta^2}{12},
\frac{\theta^6+7\theta^5+18\theta^4+18\theta^3}{24} \right\}, \end{equation*}
\begin{equation*}\left\{1,\theta, \theta^2, \frac{\theta^3+ 3\theta^2}{2}, \frac{\theta^4+ \theta^3}{6}, \frac{\theta^5+7\theta^4+6\theta^3+6\theta^2}{12},
\frac{\theta^6+7\theta^5+18\theta^4+18\theta^3}{24} \right\}, \end{equation*}is an integral basis of K.
Acknowledgement
The first author is grateful to the National Board for Higher Mathematics, Department of Atomic Energy, India for postdoctoral fellowship. The second author is thankful to the Indian National Science Academy for Honorary Scientistship.