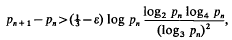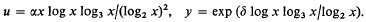Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Pomerance, Carl
1979.
The prime number graph.
Mathematics of Computation,
Vol. 33,
Issue. 145,
p.
399.
McCurley, Kevin S.
1986.
The least 𝑟-free number in an arithmetic progression.
Transactions of the American Mathematical Society,
Vol. 293,
Issue. 2,
p.
467.
Ribenboim, Paulo
1988.
The Book of Prime Number Records.
p.
153.
Maier, Helmut
and
Pomerance, Carl
1990.
Unusually large gaps between consecutive primes.
Transactions of the American Mathematical Society,
Vol. 322,
Issue. 1,
p.
201.
Pintz, János
1997.
Very Large Gaps between Consecutive Primes.
Journal of Number Theory,
Vol. 63,
Issue. 2,
p.
286.
Goto, Kazuo
1999.
On Monotone Almost (P, μ) ‐ u. d. Mod 1 Sequence.
Mathematische Nachrichten,
Vol. 205,
Issue. 1,
p.
5.
Berndt, Bruce C.
Kohnen, Winfried
and
Ono, Ken
2003.
Number Theory and Modular Forms.
Vol. 10,
Issue. ,
p.
9.
2006.
Die Welt der Primzahlen.
p.
161.
Maier, H
and
Stewart, C. L
2007.
On intervals with few prime numbers.
Journal für die reine und angewandte Mathematik (Crelles Journal),
Vol. 2007,
Issue. 608,
Ribenboim, Paulo
2011.
Die Welt der Primzahlen.
p.
163.
Raigorodskii, A. M.
2012.
On the chromatic numbers of spheres in ℝ n.
Combinatorica,
Vol. 32,
Issue. 1,
p.
111.
Narkiewicz, Władysław
2012.
Rational Number Theory in the 20th Century.
p.
131.
Pintz, János
2013.
Erdős Centennial.
Vol. 25,
Issue. ,
p.
485.
Freiberg, Tristan
2015.
Advances in the Theory of Numbers.
Vol. 77,
Issue. ,
p.
87.
Ford, Kevin
Heath-Brown, D. R.
and
Konyagin, Sergei
2015.
Analytic Number Theory.
p.
83.
He, Xiaoyu
2015.
Geometric progression-free sequences with small gaps.
Journal of Number Theory,
Vol. 151,
Issue. ,
p.
197.
Ford, Kevin
Green, Ben
Konyagin, Sergei
and
Tao, Terence
2016.
Large gaps between consecutive prime numbers.
Annals of Mathematics,
Vol. 183,
Issue. 3,
p.
935.
Vaughan, Robert C.
2016.
Open Problems in Mathematics.
p.
479.
Maynard, James
2016.
Large gaps between primes.
Annals of Mathematics,
Vol. 183,
Issue. 3,
p.
915.
Maier, Helmut
and
Rassias, Michael Th.
2017.
The ternary Goldbach problem with a prime and two isolated primes.
Proceedings of the Steklov Institute of Mathematics,
Vol. 296,
Issue. 1,
p.
183.