Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-25T20:32:26.490Z Has data issue: false hasContentIssue false
  • English
  • Français

Dense subalgebras of purely infinite simple groupoid C*-algebras

Part of: Selfadjoint operator algebras Rings and algebras arising under various constructions

Published online by Cambridge University Press:  30 March 2020

Jonathan H. Brown ,
Lisa Orloff Clark  and
Astrid an Huef
Jonathan H. Brown
Affiliation:
Department of Mathematics, University of Dayton, 300 College Park, Dayton, OH45469-2316, USA ([email protected])
Lisa Orloff Clark
Affiliation:
School of Mathematics and Statistics, Victoria University of Wellington, P.O. Box 600, Wellington6140, New Zealand ([email protected]; [email protected])
Astrid an Huef
Affiliation:
School of Mathematics and Statistics, Victoria University of Wellington, P.O. Box 600, Wellington6140, New Zealand ([email protected]; [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

A simple Steinberg algebra associated to an ample Hausdorff groupoid G is algebraically purely infinite if and only if the characteristic functions of compact open subsets of the unit space are infinite idempotents. If a simple Steinberg algebra is algebraically purely infinite, then the reduced groupoid 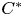$C^*$-algebra 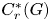$C^*_r(G)$ is simple and purely infinite. But the Steinberg algebra seems too small for the converse to hold. For this purpose we introduce an intermediate *-algebra B(G) constructed using corners 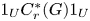$1_U C^*_r(G) 1_U$ for all compact open subsets U of the unit space of the groupoid. We then show that if G is minimal and effective, then B(G) is algebraically properly infinite if and only if 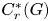$C^*_r(G)$ is purely infinite simple. We apply our results to the algebras of higher-rank graphs.

Keywords

purely infinite ringpurely infinite $C^*$-algebraample groupoidSteinberg algebraKumjian–Pask algebrainfinite projectioninfinite idempotent

MSC classification

Primary: 46L05: General theory of $C^*$-algebras
Secondary: 16S60: Rings of functions, subdirect products, sheaves of rings
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 63 , Issue 3 , August 2020 , pp. 609 - 629
Check for updates
Copyright
Copyright © Edinburgh Mathematical Society 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Abrams, G. and Aranda Pino, G., Purely infinite simple Leavitt path algebras, J. Pure Appl. Algebra 207 (2006), 553–563.CrossRefGoogle Scholar
2Anantharaman-Delaroche, C., Purely infinite C*-algebras arising from dynamical systems, Bull. Soc. Math. France 125 (1997), 199–225.CrossRefGoogle Scholar
3Ara, P., The exchange property for purely infinite simple rings, Proc. Amer. Math. Soc. 132 (2004), 2543–2547.CrossRefGoogle Scholar
4Ara, P., Goodearl, K. R. and Pardo, E., K 0 of purely infinite simple rings, K-Theory 26 (2002), 69–100.CrossRefGoogle Scholar
5Aranda Pino, G., Clark, J., an Huef, A. and Raeburn, I., Kumjian–Pask algebras of higher-rank graphs, Trans. Amer. Math. Soc. 365 (2013), 3613–3641.CrossRefGoogle Scholar
6Aranda Pino, G., Goodearl, K. R., Perera, F. and Siles Molina, M., Non-simple purely infinite rings, Amer. J. Math. 132 (2010), 563–610.CrossRefGoogle Scholar
7Bönicke, C. and Li, K., Ideal structure and pure infiniteness of ample groupoid C*-algebras, Ergodic Theory Dyn. Syst. 40 (2020), 3–63.CrossRefGoogle Scholar
8Brown, J. H., Clark, L. O., Farthing, C. and Sims, A., Simplicity of algebras associated to étale groupoids, Semigroup Forum 88 (2014), 433–452.CrossRefGoogle Scholar
9Brown, J. H., Clark, L. O. and Sierakowski, A., Purely infinite $C^*$-algebras associated to étale groupoids, Ergodic Theory Dyn. Syst. 35 (2015), 2397–2411.CrossRefGoogle Scholar
10Clark, L. O. and Edie-Michell, C., Uniqueness theorems for Steinberg algebras, Algebr. Represent. Theory 18 (2015), 907–916.10.1007/s10468-015-9522-2CrossRefGoogle Scholar
11Clark, L. O., Exel, R. and Pardo, E., A generalised uniqueness theorem and the graded ideal structure of Steinberg algebras, Forum Math. 30 (2018), 533–552.CrossRefGoogle Scholar
12Clark, L. O., Farthing, C., Sims, A. and Tomforde, M., A groupoid generalisation of Leavitt path algebras, Semigroup Forum 89 (2014), 501–517.CrossRefGoogle Scholar
13Clark, L. O., Flynn, C. and an Huef, A., Kumjian–Pask algebras of locally convex higher-rank graphs, J. Algebra 399 (2014), 445–474.CrossRefGoogle Scholar
14Clark, L. O., an Huef, A. and Sims, A., AF-embeddability of 2-graph algebras and stable finiteness of k-graph algebras, J. Funct. Anal. 271 (2016), 958–991.CrossRefGoogle Scholar
15Clark, L. O. and Pangalela, Y. E. P., Kumjian–Pask algebras of finitely-aligned higher-rank graphs, J. Algebra 482 (2017), 364–397.CrossRefGoogle Scholar
16Evans, D. G. and Sims, A., When is the Cuntz–Krieger algebra of a higher-rank graph approximately finite-dimensional? J. Funct. Anal. 263 (2012), 183–215.CrossRefGoogle Scholar
17Exel, R., Reconstructing a totally disconnected groupoid from its ample semigroup, Proc. Amer. Math. Soc. 138 (2008), 2991–3001.CrossRefGoogle Scholar
18Farthing, C., Muhly, P. and Yeend, T., Higher-rank graph -algebras: an inverse semigroup and groupoid approach, Semigroup Forum 71 (2005), 159–187.CrossRefGoogle Scholar
19González-Barroso, M. A. and Pardo, E., Structure of nonunital purely infinite simple rings, Comm. Algebra 34 (2006), 617–624.CrossRefGoogle Scholar
20an Huef, A., Kang, S. and Raeburn, I., Spatial realisations of KMS states on the -algebras of higher-rank graphs, J. Math. Anal. Appl. 427 (2015), 977–1003.CrossRefGoogle Scholar
21Kirchberg, E. and Rørdam, M., Non-simple purely infinite C*-algebras, Amer. J. Math. 122 (2000), 637–666.10.1353/ajm.2000.0021CrossRefGoogle Scholar
22Kumjian, A. and Pask, D., Higher rank graph $C^*$-algebras, New York J. Math. 6 (2000), 1–20.Google Scholar
23Larki, H., Purely infinite simple Kumjian–Pask algebras, Forum Math. 30 (2018), 253–268.CrossRefGoogle Scholar
24Murphy, G. J., C*-Algebras and operator theory (Academic Press, Boston, 1990).Google Scholar
25Pask, D., Raeburn, I., Rørdam, M. and Sims, A., Rank-two graphs whose $C^*$-algebras are direct limits of circle algebras, J. Funct. Anal. 239 (2006), 137–178.CrossRefGoogle Scholar
26Pask, D., Sierakowski, A. and Sims, A., Unbounded quasitraces, stable finiteness and pure infiniteness, Houston J. Math. 45 (2019), 763–814.Google Scholar
27Pedersen, G. K., C*-algebras and their automorphism groups (Academic Press, London, 1979).Google Scholar
28Raeburn, I., Sims, A. and Yeend, T., The C*-algebras of finitely aligned higher-rank graphs, J. Funct. Anal. 213 (2004), 206–240.CrossRefGoogle Scholar
29Rainone, T. and Sims, A., A dichotomy for groupoid $C^*$-algebras, Ergodic Theory Dyn. Syst. 40 (2020), 521–563.CrossRefGoogle Scholar
30Renault, J., A groupoid approach to -algebras, Lecture Notes in Mathematics, Volume 793 (Springer, Berlin, 1980).CrossRefGoogle Scholar
31Renault, J., Cartan subalgebras in $C^*$-algebras, Irish Math. Soc. Bull. 61 (2008), 29–63.Google Scholar
32Rørdam, M., On the structure of simple C*-algebras tensored with a UHF-algebra. II, J. Funct. Anal. 107 (1992), 255–269.CrossRefGoogle Scholar
33Rørdam, M., Larsen, F. and Lausten, N. J., An Introduction to K-theory for C*-Algebras, London Mathematical Society Student Texts, Volume 49 (Cambridge University Press, Cambridge, 2000).CrossRefGoogle Scholar
34Sims, A., Gauge-invariant ideals in the C*-algebras of finitely aligned higher-rank graphs, Canad. J. Math. 58 (2006), 1268–1290.CrossRefGoogle Scholar
35Spielberg, J., Graph-based models for Kirchberg algebras, J. Operator Theory 57 (2007), 347–374.Google Scholar
36Steinberg, B., A groupoid approach to inverse semigroup algebras, Adv. Math. 223 (2010), 689–727.CrossRefGoogle Scholar
37Webster, S. G., The path space of a higher-rank graph, Stud. Math. 204 (2011), 155–185.10.4064/sm204-2-4CrossRefGoogle Scholar
38Yeend, T., Groupoid models for the C*-algebras of topological higher-rank graphs, J. Operator Theory 51 (2007), 95–120.Google Scholar