Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Kissin, E.
and
Shulman, V. S.
1994.
Differential properties of some dense subalgebras of C*-algebras.
Proceedings of the Edinburgh Mathematical Society,
Vol. 37,
Issue. 3,
p.
399.
Kissin, Edward
1994.
Superderivations ofC *-algebras implemented by symmetric operators.
Communications in Mathematical Physics,
Vol. 160,
Issue. 2,
p.
333.
Badea, C.
1998.
The Stable Rank of Topological Algebras and a Problem of R. G. Swan.
Journal of Functional Analysis,
Vol. 160,
Issue. 1,
p.
42.
Kissin, Edward
and
Shulman, Victor S
1998.
Differential Banach *-Algebras of Compact Operators Associated with Symmetric Operators.
Journal of Functional Analysis,
Vol. 156,
Issue. 1,
p.
1.
Kissin, Edward
and
Shulman, Victor S.
1999.
Dual spaces and isomorphisms of some differential Banach ∗-algebras of operators.
Pacific Journal of Mathematics,
Vol. 190,
Issue. 2,
p.
329.
2005.
Topological Algebras with Involution.
Vol. 200,
Issue. ,
p.
451.
Kissin, Edward
and
Shulman, Victor
2006.
LIPSCHITZ FUNCTIONS ON HERMITIAN BANACH *-ALGEBRAS.
The Quarterly Journal of Mathematics,
Vol. 57,
Issue. 2,
p.
215.
Elliott, George A.
and
Li, Hanfeng
2007.
Morita equivalence of smooth noncommutative tori.
Acta Mathematica,
Vol. 199,
Issue. 1,
p.
1.
Elliott, George A.
and
Li, Hanfeng
2008.
Strong Morita equivalence of higher-dimensional noncommutative tori. II.
Mathematische Annalen,
Vol. 341,
Issue. 4,
p.
825.
Romero, José Luis
2009.
Explicit Localization Estimates for Spline-Type Spaces.
Sampling Theory in Signal and Image Processing,
Vol. 8,
Issue. 3,
p.
249.
Gröchenig, Karlheinz
and
Klotz, Andreas
2010.
Noncommutative Approximation: Inverse-Closed Subalgebras and Off-Diagonal Decay of Matrices.
Constructive Approximation,
Vol. 32,
Issue. 3,
p.
429.
Klotz, Andreas
2012.
Spectral invariance of Besov–Bessel subalgebras.
Journal of Approximation Theory,
Vol. 164,
Issue. 2,
p.
268.
Azmi, Fatima M.
2012.
Differential Fréchet $*$-algebras and characterization of smooth functions on ${\bf R}$.
Rocky Mountain Journal of Mathematics,
Vol. 42,
Issue. 6,
BHATT, SUBHASH J
KARIA, DINESH J
and
SHAH, MEETAL M
2013.
On a class of smooth Frechet subalgebras of C * -algebras.
Proceedings - Mathematical Sciences,
Vol. 123,
Issue. 3,
p.
393.
Gröchenig, Karlheinz
and
Klotz, Andreas
2014.
Norm‐controlled inversion in smooth Banach algebras, II.
Mathematische Nachrichten,
Vol. 287,
Issue. 8-9,
p.
917.
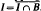 .
.