No CrossRef data available.
Published online by Cambridge University Press: 22 November 2024
In this paper, we establish a second main theorem for holomorphic maps with finite growth index on complex discs intersecting arbitrary families of hypersurfaces (fixed and moving) in projective varieties, which gives an above bound of the sum of truncated defects. Our result also generalizes and improves many previous second main theorems for holomorphic maps from 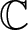 ${\mathbb{C}}$ intersecting hypersurfaces (moving and fixed) in projective varieties.
${\mathbb{C}}$ intersecting hypersurfaces (moving and fixed) in projective varieties.