Published online by Cambridge University Press: 15 January 2020
Let Φ be a finite-dimensional algebra over a field k. Kleiner described the Auslander–Reiten sequences in a precovering extension closed subcategory 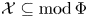 ${\rm {\cal X}}\subseteq {\rm mod }\,\Phi $. If
${\rm {\cal X}}\subseteq {\rm mod }\,\Phi $. If 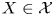 $X\in \mathcal {X}$ is an indecomposable such that
$X\in \mathcal {X}$ is an indecomposable such that  ${\rm Ext}_\Phi ^1 (X,{\rm {\cal X}})\ne 0$ and
${\rm Ext}_\Phi ^1 (X,{\rm {\cal X}})\ne 0$ and 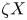 $\zeta X$ is the unique indecomposable direct summand of the
$\zeta X$ is the unique indecomposable direct summand of the 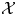 $\mathcal {X}$-cover
$\mathcal {X}$-cover 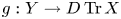 $g:Y\to D\,{\rm Tr}\,X$ such that
$g:Y\to D\,{\rm Tr}\,X$ such that 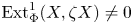 ${\rm Ext}_\Phi ^1 (X,\zeta X)\ne 0$, then there is an Auslander–Reiten sequence in
${\rm Ext}_\Phi ^1 (X,\zeta X)\ne 0$, then there is an Auslander–Reiten sequence in 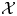 $\mathcal {X}$ of the form
$\mathcal {X}$ of the form
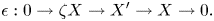 $${\rm \epsilon }:0\to \zeta X\to {X}^{\prime}\to X\to 0.$$
$${\rm \epsilon }:0\to \zeta X\to {X}^{\prime}\to X\to 0.$$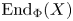 ${\rm En}{\rm d}_\Phi (X)$ modulo the morphisms factoring through a projective is a division ring, Kleiner proved that each non-split short exact sequence of the form
${\rm En}{\rm d}_\Phi (X)$ modulo the morphisms factoring through a projective is a division ring, Kleiner proved that each non-split short exact sequence of the form
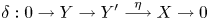 $$\delta :0\to Y\to {Y}^{\prime}\buildrel \eta \over \longrightarrow X\to 0$$
$$\delta :0\to Y\to {Y}^{\prime}\buildrel \eta \over \longrightarrow X\to 0$$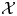 $\mathcal {X}$, and the pushout of δ along g gives an Auslander–Reiten sequence in
$\mathcal {X}$, and the pushout of δ along g gives an Auslander–Reiten sequence in 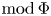 ${\rm mod}\,\Phi $ ending at X.
${\rm mod}\,\Phi $ ending at X.
In this paper, we give higher-dimensional generalizations of this. Let 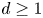 $d\geq 1$ be an integer. A d-cluster tilting subcategory
$d\geq 1$ be an integer. A d-cluster tilting subcategory 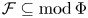 ${\rm {\cal F}}\subseteq {\rm mod}\,\Phi $ plays the role of a higher
${\rm {\cal F}}\subseteq {\rm mod}\,\Phi $ plays the role of a higher 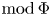 ${\rm mod}\,\Phi $. Such an
${\rm mod}\,\Phi $. Such an 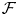 $\mathcal {F}$ is a d-abelian category, where kernels and cokernels are replaced by complexes of d objects and short exact sequences by complexes of d + 2 objects. We give higher versions of the above results for an additive ‘d-extension closed’ subcategory
$\mathcal {F}$ is a d-abelian category, where kernels and cokernels are replaced by complexes of d objects and short exact sequences by complexes of d + 2 objects. We give higher versions of the above results for an additive ‘d-extension closed’ subcategory 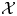 $\mathcal {X}$ of
$\mathcal {X}$ of 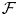 $\mathcal {F}$.
$\mathcal {F}$.