Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-26T13:08:18.377Z Has data issue: false hasContentIssue false
  • English
  • Français

A cross-constrained variational problem for the generalized Davey–Stewartson system

Part of: Equations of mathematical physics and other areas of application Partial differential equations

Published online by Cambridge University Press:  02 February 2009

Zaihui Gan  and
Jian Zhang
Zaihui Gan
Affiliation:
College of Mathematics and Software Science, Sichuan Normal University, Chengdu 610068, People's Republic of China ([email protected])
Jian Zhang
Affiliation:
College of Mathematics and Software Science, Sichuan Normal University, Chengdu 610068, People's Republic of China ([email protected])
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study the sharp threshold for blow-up and global existence and the instability of standing wave eiωtuω(x) for the Davey–Stewartson system

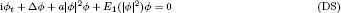
in ℝ3, where uω is a ground state. By constructing a type of cross-constrained variational problem and establishing so-called cross-invariant manifolds of the evolution flow, we derive a sharp criterion for global existence and blow-up of the solutions to (DS), which can be used to show that there exist blow-up solutions of (DS) arbitrarily close to the standing waves.

Keywords

generalized Davey–Stewartson systemcross-constrained variational problemsharp thresholdglobal existenceblow-upinstability

MSC classification

Secondary: 35A15: Variational methods 35Q55: NLS-like equations (nonlinear Schrödinger) 35B30: Dependence of solutions on initial and boundary data, parameters
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 52 , Issue 1 , February 2009 , pp. 67 - 77
Copyright
Copyright © Edinburgh Mathematical Society 2009