Hostname: page-component-745bb68f8f-5r2nc Total loading time: 0 Render date: 2025-01-13T08:30:03.305Z Has data issue: false hasContentIssue false
  • English
  • Français

A criterion for absolute Cesàro summability of negative order of a Fourier series

Published online by Cambridge University Press:  20 January 2009

Yung-Ming Chen
Yung-Ming Chen
Affiliation:
Depart of Mathematics, University of Hong Kong
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let f(x) be integrable L(0, 2π) and periodic with period 2π, and let ψ(t) be the conjugate function of 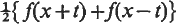with respect to the variable t, where x is onsidered as an arbitrary constant. The following theorems are due to K. K. Chen (1), (2), pp. 111–124.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 14 , Issue 4 , December 1965 , pp. 311 - 319
Copyright
Copyright © Edinburgh Mathematical Society 1965

References

REFERENCES

(1) Chen, K. K.On the absolute Cesaro summability of negative order for a Fourier series at a given point. Amer. J. Math. 66 (1944), 299–312.CrossRefGoogle Scholar
(2) Chen, K. K.Summation of the Fourier Series of Orthogonal Functions (Peking, 1957).Google Scholar
(3) Chow, H. C.Note on the absolute Cesaro summability of power series. Proc. London Math. Soc. (2) 43 (1937), 484–489.Google Scholar
(4) Chow, H. C.The absolute summability of Fourier series. J. London Math. Soc. 17 (1942), 17–23.CrossRefGoogle Scholar
(5) Flett, T. M.On an extension of absolute summability and some theorems of Littlewood and Paley. Proc. London Math. Soc. (3) 7 (1957), 113–141.CrossRefGoogle Scholar
(6) Flett, T. M.On the absolute summability of a Fourier series and its con- jugate series. Proc. London Math. Soc. (3) 8 (1958), 257–311.Google Scholar
(7) vFLETT, T. M.Some more theorems concerning the absolute summability of Fourier series and power series. Proc. London Math. Soc. (3) 8 (1958), 359–387.Google Scholar
(8) Hardy, G. H. and Littlewood, J. E.A convergence criterion for Fourier series. Math. Zeitschrift, 28, (1928), 612–634.CrossRefGoogle Scholar
(9) Hardy, G. H. and Littlewood, J. E.Some properties of fractional integrals, I. Math. Zeitschrift, 27 (1928), 565–606.CrossRefGoogle Scholar
(10) Hyslop, J. M.On the absolute summability of Fourier series. Proc. London Math. Soc. (2) 43 (1937), 475–483.Google Scholar
(11) Kogbetliantz, E.Sur les series absolument sommables par la mdthode des moyennes arithméique. Bull, des Sci. Math. (2) 49 (1925), 234–256.Google Scholar
(12) Zygmund, A.Remarque sur la convergence absolue des series de Fourier. J. London Math. Soc. 3 (1928), 194–196.CrossRefGoogle Scholar