Hostname: page-component-77c89778f8-5wvtr Total loading time: 0 Render date: 2024-07-17T10:36:53.223Z Has data issue: false hasContentIssue false
  • English
  • Français

A counterexample of hermitian liftings

Published online by Cambridge University Press:  20 January 2009

Pei-Kee Lin
Pei-Kee Lin
Affiliation:
Department of Mathematical Sciences, Memphis State University, Memphis, TN 38152, U.S.A.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let X be a complex Banach space, and let 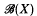and 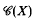denote respectively the algebras of bounded and compact operators on X. The quotient algebra 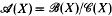is called the Calkin algebra associated with X. It is known that both 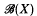and 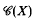are complex Banach algebras with unit e. For such unital Banach algebras B, set

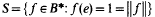
and define the numerical range of x ∈ B as

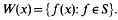
x is said to be hermitian if W(x)⊆R. It is known that

Fact 1. ([4 vol. I, p. 46]) x is hermitian if and only if ‖eiαx‖ = (or ≦)1 for all α ∈ R, where ex is defined by

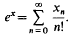
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 32 , Issue 2 , June 1989 , pp. 255 - 259
Copyright
Copyright © Edinburgh Mathematical Society 1989

References

REFERENCES

1.Allen, G. D., Legg, D. A. and Ward, J. D., Hermitian liftings in Orlicz sequence spaces, Pacific J. Math. 86 (1986), 379–387.CrossRefGoogle Scholar
2.Allen, G. D., Legg, D. A. and Ward, J. D., Essentially hermitian operators in B(Lp), Proc. Amer. Math. Soc. 80 (1980), 71–77.Google Scholar
3.Allen, G. D. and Ward, J. D., Hermitian liftings in B(lp), J. Operator Theory 1 (1979), 27–36.Google Scholar
4.Bonsall, F. F. and Duncan, J., Numerical Ranges of Operators on Normed Spaces and of Elements of Normed Algebras, I, II (Cambridge University Press, Cambridge, 1971, 1973).CrossRefGoogle Scholar
5.Fleming, R. J. and Jamison, J. E., Hermitian and adjoint abelian operators on certain Banach spaces, Pacific J. Math. 52 (1974), 67–85.CrossRefGoogle Scholar
6.Legg, D. A., A counterexample in the theory of Hermitian liftings, Proc. Edinburgh Math. Soc. 25 (1982), 141–144.Google Scholar
7.Legg, D. A. and Ward, J. D., Essentially Hermitian operators on l 1 are compact perturbations of hermitians, Proc. Amer. Math. Soc. 67 (1977), 224–226.Google Scholar
8.Lin, Pei-Kee, The isometries of L 2(Ώ,X), preprint.Google Scholar
9.Lindenstrauss, J. and Tzafriri, L., Classical Banach Spaces I, Sequence Spaces (Springer-Verlag, Berlin-Heidelberg-New York, 1977).Google Scholar