Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-26T09:07:22.795Z Has data issue: false hasContentIssue false
  • English
  • Français

Cotorsion pairs and model structures on Ch(R)

Part of: Homological algebra Commutative algebra: Homological methods

Published online by Cambridge University Press:  17 August 2011

Gang Yang  and
Zhongkui Liu
Gang Yang
Affiliation:
School of Mathematics, Physics and Software Engineering, Lanzhou Jiaotong University, Lanzhou 730070, People's Republic of China ([email protected]) College of Mathematics and Information Science, Northwest Normal University, Lanzhou 730070, People's Republic of China ([email protected])
Zhongkui Liu
Affiliation:
College of Mathematics and Information Science, Northwest Normal University, Lanzhou 730070, People's Republic of China ([email protected])
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

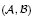We show that if the given cotorsion pair in the category of modules is complete and hereditary, then both of the induced cotorsion pairs in the category of complexes are complete. We also give a cofibrantly generated model structure that can be regarded as a generalization of the projective model structure.

Keywords

(pre)envelopes(pre)coverscotorsion pairsprojective dimension of complexesmodel structures

MSC classification

Secondary: 13D05: Homological dimension 13D07: Homological functors on modules (Tor, Ext, etc.) 18G15: Ext and Tor, generalizations, Künneth formula 18G35: Chain complexes 18G55: Homotopical algebra
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 54 , Issue 3 , October 2011 , pp. 783 - 797
Copyright
Copyright © Edinburgh Mathematical Society 2011

References

1.Akinci, K. D. and Alizade, R., Special precovers in cotorsion theories, Proc. Edinb. Math. Soc. 45 (2002), 411–420.Google Scholar
2.Aldrich, S. T. and Enochs, E. E., Envelopes and covers by modules of finite injective and projective dimensions, J. Alg. 242 (2001), 447–459.Google Scholar
3.Aldrich, S. T., Enochs, E. E., Rozas, J. R. García and Oyonarte, L., Covers and envelopes in Groththendieck categories: flat cover of complexes with applications, J. Alg. 243 (2001), 615–630.Google Scholar
4.Anderson, F. W. and Fuller, K. R., Rings and categories of modules, 2nd edn, Graduate Texts in Mathematics, Volume 13 (Springer, 1992).Google Scholar
5.Avramov, L. L. and Foxby, H.-B., Homological dimensions of unbounded complexes, J. Pure Appl. Alg. 71 (1991), 129–155.CrossRefGoogle Scholar
6.Bican, L., Bashir, R. El and Enochs, E., All modules have flat covers, Bull. Lond. Math. Soc. 33 (2001), 385–390.CrossRefGoogle Scholar
7.Christensen, L. W., Gorenstein dimensions, Lecture Notes in Mathematics, Volume 1747 (Springer, 2000).Google Scholar
8.Ding, N. Q. and Chen, J. L., Relative covers and envelopes, Acta Math. Sinica 41(3) (1998), 609–616 (in Chinese).Google Scholar
9.Dwyer, W. G. and Spalinski, J., Homotopy theories and model categories, in Handbook of algebraic topology, pp. 73–126 (North-Holland, Amsterdam, 1995).Google Scholar
10.Eklof, P. C., Homological algebra and set theory, Trans. Am. Math. Soc. 227 (1977), 207–225.Google Scholar
11.Eklof, P. C. and Trlifaj, J., How to make Ext vanish, Bull. Lond. Math. Soc. 33 (2001), 41C51CrossRefGoogle Scholar
12.Enochs, E. E. and Iacob, A., The ℵ1-product of DG-injective complexes, Proc. Edinb. Math. Soc. 49 (2006), 257–266.Google Scholar
13.Enochs, E. E. and Jenda, O. M. G., Relative homological algebra, De Gruyter Expositions in Mathematics, Volume 30 (Walter de Gruyter, Berlin, 2000).Google Scholar
14.Enochs, E. E., Jenda, O. M. G. and Xu, J. Z., Orthogonality in the category of complexes, Math. J. Okayama Univ. 38(1) (1996), 25–46.Google Scholar
15.Enochs, E. E. and Oyonarte, L., Covers, envelopes and cotorsion theories (Hauppauge, New York, 2002).Google Scholar
16.Rozas, J. R. García, Covers and envelopes in the category of complexes of modules, Research Notes in Mathematics (Chapman and Hall/CRC, Boca Raton, FL, 1999).Google Scholar
17.Gillespie, J., The flat model structure on Ch(R), Trans. Am. Math. Soc. 356(8) (2004), 3369–3390.CrossRefGoogle Scholar
18.Gillespie, J., Kaplansky classes and derived categories, Math. Z. 257 (2007), 811–843.CrossRefGoogle Scholar
19.Gillespie, J., Cotorsion pairs and degreewise homological model structures, Homology Homotopy Applic. 10(1) (2008), 283–304.CrossRefGoogle Scholar
20.Hovey, M., Model categories (American Mathematical Society, Providence, RI, 1999).Google Scholar
21.Hovey, M., Cotorsion pairs, model category structures, and representation theory, Math. Z. 241 (2002), 553–592.Google Scholar
22.Mao, L. X. and Ding, N. Q., Envelopes and covers by modules of finite FP-injective and flat dimensions, Commun. Alg. 35 (2007), 833–849.Google Scholar
23.Salce, L., Cotorsion theories for abelian groups, Symp. Math. 13 (1979), 11–32.Google Scholar
24.Trlifaj, J., Covers, envelopes, and cotorsion theories, Lecture Notes for the Workshop ‘Homological Methods in Module Theory’, Cortona, 10-16 September 2000 (available at www.karlin.mff.cuni.cz/~trlifaj/cortona.pdf).Google Scholar