Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-26T01:11:22.001Z Has data issue: false hasContentIssue false
  • English
  • Français

The Convergence of the Series in Mathieu's Functions

Published online by Cambridge University Press:  20 January 2009

G. N. Watson
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Periodic solutions of Mathieu's equation*

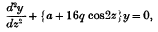
where a is a suitable function of q have recently been discussed in several papers in these Proceedings. An elegant method of determining these solutions, which are written

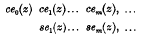
was given by Whittaker, † who obtained the integral equation

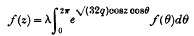
which is satisfied by periodic solutions of Mathieu's equation.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 33 , February 1914 , pp. 25 - 30
Copyright
Copyright © Edinburgh Mathematical Society 1914

References

* Liouville's Journal, sér. 2, t. XIII., pp. 137–203.Google Scholar

† Proceedings of the Mathematical Congress, 1912, vol. 1.Google Scholar

* The first of these does not seem to have been noticed previously; it would not be obvious from Mathieu's method, and Whittaker's method does not introduce a at all

* This is the reason for introducing the factor (–)γ.

* See Bromwich, , Infinite Series, p. 67.Google Scholar It is obvious that C n, o=B n 0.