No CrossRef data available.
Article contents
Conics on a Maschke Surface
Published online by Cambridge University Press: 20 January 2009
Extract
The six quaternary quartic forms
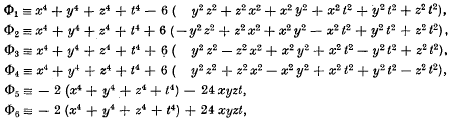
were first obtained by Maschke; it has recently been explained that the quartic surfaces obtained by equating these forms to zero are important constituents of Klein's famous configuration derived from six linear complexes that are mutually in involution. The quartic surface Φi = 0 will be denoted, for each of the six suffixes i, by Mi.
- Type
- Research Article
- Information
- Proceedings of the Edinburgh Mathematical Society , Volume 7 , Issue 3 , February 1946 , pp. 153 - 161
- Copyright
- Copyright © Edinburgh Mathematical Society 1946
References
page 153 note 1 Math. Annalen, 17 (1880), 510–516.CrossRefGoogle Scholar
page 153 note 2 Proc. Edin. Math. Soc. (2), 7 (1945), 93–103. This paper will be alluded to as E.CrossRefGoogle Scholar
page 153 note 3 The notation for the tetrahedra which was used in E is brought into line by replacing the suffix 0 by 5 and T i by U i6.Google Scholar
page 159 note 1 Journal für Math., 58 (1861), 93–108 (105).Google Scholar


