Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-26T00:59:34.447Z Has data issue: false hasContentIssue false
  • English
  • Français

Concentration of the error between a function and its polynomial of best uniform approximation

Published online by Cambridge University Press:  20 January 2009

Maurice Hasson
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let f be a continuous real valued function defined on [−1, 1] and let En(f) denote the degree of best uniform approximation to f by algebraic polynomial of degree at most n. The supremum norm on [a, b] is denoted by ∥.∥[a, b] and the polynomial of degree n of best uniform approximation is denoted by Pn. We find a class of functions f such that there exists a fixed a ∈(−1, 1) with the following property

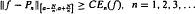
for some positive constants C and N independent of n. Moreover the sequence 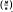is optimal in the sense that if 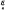is replaced by then the above inequality need not hold no matter how small C > 0 is chosen.

We also find another, more general class a functions f for which

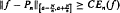infinitely often.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 41 , Issue 3 , October 1998 , pp. 447 - 463
Copyright
Copyright © Edinburgh Mathematical Society 1998

References

REFERENCES

1. Bernstein, S., Sur la meilleure approximation de |x| par des polynômes de degrés donnés, Acta Math. 37 (1914), 1–57.CrossRefGoogle Scholar
2. Borwein, P. B., Kroó, A., Grothmann, R. and Saff, E. B., The density of alternation points in rational approximation, Proc. Amer. Math. Soc. 105 (1989), 881–888.CrossRefGoogle Scholar
3. Kadek, M. I., On the distribution of points of maximal deviation in the approximation of continuous functions by polynomials, Uspekhi Mat. Nauk 15 (1960), 199–202.Google Scholar
4. Kroó, A. and Peherstorfer, F., On the asymptotic distribution of oscillation points in rational approximation, Anal. Math. 3 (1993), 225–232.CrossRefGoogle Scholar
5. Lorentz, G. G., Golitschek, M. v. and Makovoz, Y., Constructive Approximation (Advanced Problems, Springer, New York, 1996).CrossRefGoogle Scholar
6. Lorentz, G. G., Distribution of alternating points in uniform approximation, Proc. Amer. Math. Soc. 92 (1984), 401–403.CrossRefGoogle Scholar
7. Nikol'skii, S. M., On the best approximation of functions, the sth derivative of which has discontinuities of the first kind, Dokl. Akad. Nauk. USSR 55 (1947), 99–102.Google Scholar
8. Steckin, V. A., On the order of the best approximation of continuous functions, Izv. Akad. Nauk. USSR 15 (1951), 219–242.Google Scholar
9. Szegö, G., Orthogonal Polynomials, 4th edn. (Amer. Math. Soc., Providence, 1975).Google Scholar
10. Tashev, S., On the distribution of the points of maximal deviation for the polynomials of best Chebyshev and Hausdorff approximations, in Approximation and Function Spaces (North-Holland, Amsterdam, New York, 1981), 791–799.Google Scholar
11. Timan, A. F., Theory of Approximation of Functions of a Real Variable (MacMillan, New York, 1963).Google Scholar
12. Zygmund, A., Smooth functions, Duke Math. J. 12 (1945), 47–76.CrossRefGoogle Scholar