Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-24T19:01:23.476Z Has data issue: false hasContentIssue false
  • English
  • Français

Complex inversion formula for the distributional Stieltjes transform

Published online by Cambridge University Press:  20 January 2009

Stevan Pilipović
Stevan Pilipović
Affiliation:
Institute of Mathematics, University of Novi Sad, Yugoslavia
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

There are several approaches to the Stieltjes transform of generalized functions ([1, 10, 5, 6, 3, 2]). In this paper we use the definition of the distributional Stieltjes transform of index ρ (ρ ∈ ℝ\(−ℕ0); ℕ0 = ℕ∪{0}), Sρ-transform, given by Lavoine and Misra [3]. The Sρ-transform is defined for a subspace of the Schwartz space 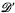(ℝ) while in [10, 5, 6, 2] the Stieltjes transform is defined for the elements of appropriate spaces of generalized functions. In these spaces differentiation is not defined which means that the Stieltjes transform of some important distributions, for example δ(k)(x − a), a≧0, k ∈ ℕ, is meaningless in the sense of [10, 5, 6, 2]. It is easy to see that the distributions δ(k)(x − a), a≧0, k ∈ ℕ, have the Sρ-transform for ρ>−k, ρ∈ℝ\(−ℕ0). These facts favour the approach to the Stieltjes transform given in [3].

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 30 , Issue 3 , October 1987 , pp. 363 - 371
Copyright
Copyright © Edinburgh Mathematical Society 1987

References

REFERENCES

1.Benedetto, J. J., Analytic representation of generalised functions, Math. Z. 97 (1967), 303–319.CrossRefGoogle Scholar
2.Erdelyi, A., Stieltjes transform of generalized functions, Proc. Roy. Soc. Edinburgh 76A (1977), 231–249.CrossRefGoogle Scholar
3.Lavoine, J. and Misra, O. P., Theoremes abeliens pour la transformation de Stieltjes des distributions, C.R. Acad. Sci. Paris, Serie A 279 (1974), 99–102.Google Scholar
4.Lavoine, J. and Misra, O. P., Abelian theorems for the distributional Stieltjes transformation, Math. Proc. Cambridge Philos. Soc. 86 (1979), 287–293.CrossRefGoogle Scholar
5.Misra, O. P., Some Abelian theorems for distributional Stieltjes transformation, J. Math. Anal. Appl. 39 (1972), 590–599.CrossRefGoogle Scholar
6.Pandey, J. N., On the Stieltjes transform of generalized functions, Math. Proc. Cambridge Philos. Soc. 71 (1971), 85–96.CrossRefGoogle Scholar
7.Pathak, R. S., A distributional generalized Stieltjes transformation, Proc. Edinburgh Math. Soc. 70 (1976), 15–22.Google Scholar
8.Pilipovic, S., An inversion theorem for the distributional Stieltjes transformation of distributions, Proc. Edinburgh Math. Soc, 29 (1986), 171–185.CrossRefGoogle Scholar
9.Sumner, D. B., An inversion formula for the generalized Stieltjes transform, Bull. Amer. Math. Soc. 55 (1949), 174–183.Google Scholar
10.Zemanian, A. H., Generalized Integral Transformations (Interscience, New York, 1968).Google Scholar