Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-28T06:39:03.117Z Has data issue: false hasContentIssue false
  • English
  • Français

Completely bounded isomorphisms of injective von Neumann algebras

Published online by Cambridge University Press:  20 January 2009

Erik Christensen  and
Allan M. Sinclair
Erik Christensen
Affiliation:
Matematisk Institut, Kobenhavn Universitet, Universitetsparken 5, 2100 Kobenhavn, Denmark
Allan M. Sinclair
Affiliation:
Department of Mathematics, University of Edinburgh, James Clerk Maxwell Building, King's Buildings, Edinburgh EH9 3JZScotland
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Milutin's Theorem states that if X and Y are uncountable metrizable compact Hausdorff spaces, then C(X) and C(Y) are isomorphic as Banach spaces [15, p. 379]. Thus there is only one isomorphism class of such Banach spaces. There is also an extensive theory of the Banach–Mazur distance between various classes of classical Banach spaces with the deepest results depending on probabilistic and asymptotic estimates [18]. Lindenstrauss, Haagerup and possibly others know that as Banach spaces

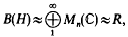
where H is the infinite dimensional separable Hilbert space, R is the injective II 1-factor on H, and ≈ denotes Banach space isomorphism. Haagerup informed us of this result, and suggested considering completely bounded isomorphisms; it is a pleasure to acknowledge his suggestion. We replace Banach space isomorphisms by completely bounded isomorphisms that preserve the linear structure and involution, but not the product. One of the two theorems of this paper is a strengthened version of the above result: if N is an injective von Neumann algebra with separable predual and not finite type I of bounded degree, then N is completely boundedly isomorphic to B(H). The methods used are similar to those in Banach space theory with complete boundedness needing a little care at various points in the argument. Extensive use is made of the conditional expectation available for injective algebras, and the methods do not apply to the interesting problems of completely bounded isomorphisms of non-injective von Neumann algebras (see [4] for a study of the completely bounded approximation property).

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 32 , Issue 2 , June 1989 , pp. 317 - 327
Copyright
Copyright © Edinburgh Mathematical Society 1989

References

REFERENCES

1.Christensen, E., Derivations and their relation to perturbations of operator algebras, Proc. Sympos. Pure Math. 38 (1982) 2, 261–;273.Google Scholar
2.Christensen, E., Perturbations of operator algebras II, Indiana Univ. Math. J. 26 (1977), 891–904.CrossRefGoogle Scholar
3.Connes, A., Classification of injective factors, Ann. of Math. 104 (1976), 73–116.Google Scholar
4.Cowling, M. and Haagerup, U., Completely bounded multipliers of the Fourier algebra of a simple Lie group of real rank one, preprint.Google Scholar
5.Dixmier, J.Les algebres d'operateurs dans I'espace Hilbertien, 2nd edition (Gauthier-Villars, Paris, 1969).Google Scholar
6.Haagerup, U.,Group C*-algebras without the completely bounded approximation property, in preparation.Google Scholar
7.Johnson, B.E., Perturbations of Banach algebras, Proc. London Math. Soc. 34 (1977), 439–458.Google Scholar
8.Kadison, R. V., Isometries of operator algebras, Ann. of Math. 54, (1951), 325–338.CrossRefGoogle Scholar
9.Kadison, R. V., and Ringrose, J. R., Fundamentals of the theory of operator algebras,, 2, (Academic Press, New York, 1986).Google Scholar
10.Lindenstrauss, J., and Tzafriri, L., Classical Banach Spaces, Sequence Spaces, (Ergebnisse 92, Springer Verlag, 1977).Google Scholar
11.Murray, F. J. and Von Neumann, J., On rings of operators, Ann. of Math. 37 (1936), 116–229.Google Scholar
12.Paulsen, V. I., Completely bounded maps and dilations. (Pitman Research Notes in Mathematics, Longman, London 1986).Google Scholar
13.Ruan, Z., Subspaces of C*-albegras, J. Funct. Anal. 76 (1988), 217–230.Google Scholar
14.Rosenthal, H. P., On injective Banach spaces and the spaces U°((i) for finite measures /i, Ada Math. 124 (1970), 205–248.Google Scholar
15.Semadeni, Z., Banach spaces of continuous functions (PWN, Warsaw, 1971).Google Scholar
16.Szankowski, A., B(H) does not have the approximation property, Acta Math. 147 (1981), 89–108.Google Scholar
17.Takesaki, M., Theory of operator algebras I (Springer Verlag, Berlin, 1979).Google Scholar
18.Tomczack-Jaegerman, N., Banach-Mazur distances … (Pitman, London, 1988).Google Scholar
19.Wassermann, S., On tensor products of certain group C*-algebras, J. Funct. Anal. 23 (1976), 239–254.CrossRefGoogle Scholar
20.Robertson, A. G. and Wassermann, S., Completely bounded isomorphisms of injective operator systems, Bull. London Math. Soc. 21 (1989) to appear.Google Scholar