Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-26T00:24:27.591Z Has data issue: false hasContentIssue false
  • English
  • Français

Completely bounded Banach-Mazur distance†

Published online by Cambridge University Press:  20 January 2009

Chun Zhang
Chun Zhang
Affiliation:
Department of Mathematics, The University of Houston, Houston, TX 77204, U.S.A.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Analogous to the Banach-Mazur distance between Banach spaces, we study the completely bounded Banach-Mazur distance between operator spaces.

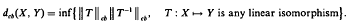
In many cases of Banach spaces and Hilbert spaces we show that the infimum is attained when T is the identity map, and X, Y have the same base space. This provides a machinery to compute and estimate dcb(X, Y). Later, using symmetric norming functions we construct counterexamples to show that distinct infinite dimensional homogeneous operator spaces may have finite cb-distance, and that two homogeneous Hilbertian operator spaces may not coincide even if they coincide over all 2-dimensional subspaces.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 40 , Issue 2 , June 1997 , pp. 247 - 260
Copyright
Copyright © Edinburgh Mathematical Society 1997

Footnotes

†

This is part of author's Ph.D. thesis directed by Professor Vern Paulsen. The author wants to express his sincerest gratitude.

References

REFERENCES

1. Bergh, J. and Lofstrom, J., Interpolation spaces (Springer-Verlag, Berlin, Heidelberg, New York, 1976).CrossRefGoogle Scholar
2. Blecher, D. P., The standard dual of an operator space, Pacific J. Math. 153 (1992), 15–30.CrossRefGoogle Scholar
3. Blecher, D. P. and Paulsen, V. I., Tensor products of operator spaces, J. Funct. Anal. 99 (1991), 262–292.CrossRefGoogle Scholar
4. Douglas, R. G., Banach Algebra Techniques in Operator Theory (Academic Press, 1972).Google Scholar
5. Effros, E. G., Advances in quantized functional analysis, in Proceedings, International Congress of Mathematicians Berkeley, 1986 (American Mathematical Society, 1987).Google Scholar
6. Effros, E. G. and Ruan, Z. J., Self-duality for the Haagerup tensor product and Hilbert space factorization, J. Funct. Anal. 100 (1991), 157–184.CrossRefGoogle Scholar
7. Goberg, I. C. and Krein, M. G., Introduction to the Theory of Linear Non-selfadjoint Operators (Transl. Math. Monographs 18 (1969)).CrossRefGoogle Scholar
8. Kadison, R. V. and Ringrose, J. R., Fundamentals of the Theory of Operator Algebras (Academic Press 100–I (1983)).Google Scholar
9. Mathes, B., A completely bounded view of Hilbert-Schmidt operators, Houston Math. J. 17(1991), 404–418.Google Scholar
10. Mathes, B., Characterizations of row and column Hilbert spaces, J. London Math. Soc., to appear.Google Scholar
11. Mathes, B. and Paulsen, V. I., Operator ideals and operator spaces, Proc. Amer. Math. Soc, to appear.Google Scholar
12. Paulsen, V. I., Completely bounded maps and dilations (Pitman Research Notes in Math. Series 146).Google Scholar
13. Paulsen, V. I., Representations of function algebras, abstract operator spaces, and Banach space geometry, J. Funct. Anal. 109 (1992), 113–129.CrossRefGoogle Scholar
14. Pisier, G., The operator Hilbert space and complex interpolation, preprint.Google Scholar
15. Pisier, G., On the local theory of operator spaces, preprint.Google Scholar
16. Pisier, G., The operator Hilbert space OH, complex interpolation and tensor norms (Lecture Notes, Texas A & M University).Google Scholar
17. Ruan, Z.-J., Subspaces of C*-algebras, J. Funct. Anal. 76 (1988), 217–230.CrossRefGoogle Scholar
18. Wojtaszczyk, P., Banach Spaces for Analysts (Cambridge University Press, 1991).CrossRefGoogle Scholar