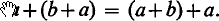Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-26T00:49:18.776Z Has data issue: false hasContentIssue false
  • English
  • Français

Commutative non-associative number theory

Published online by Cambridge University Press:  20 January 2009

M. W. Bunder
M. W. Bunder
Affiliation:
University of Wollongong, N.S.W., Australia
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Trevor Evans in (8) introduced postulates for a non-associative number theory similar to, but less general than, those of A. Robinson (9). Evans' number theory is also non-commutative under addition and multiplication, but an alternative equality axiom also suggested by Robinson leads to a number theory which is commutative under addition and still non-associative except in the special case:

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 20 , Issue 2 , September 1976 , pp. 133 - 136
Copyright
Copyright © Edinburgh Mathematical Society 1976

References

REFERENCES

(1) Etherington, I. M. H., On non-associative combinations, Proc. Roy. Soc. Edinburgh 59 (1939), 153–162.Google Scholar
(2) Etherington, I. M. H., Non-associative algebra and the symbolism of genetics, Proc. Roy. Soc. Edinburgh Sect. B 61 (1941), 24–42.Google Scholar
(3) Etherington, I. M. H., Some problems of non-associative combinations (1), Edin. Math. Notes 32 (1941), 1–6.Google Scholar
(4) Etherington, I. M. H., Some non-associative algebras in which the multiplication of indices is commutative, J. Lond. Math. Soc. 16 (1941), 48–55.Google Scholar
(5) Etherington, I. M. H., Non-associative arithmetics, Proc. Roy. Soc. Edinburgh Sect. A 62 (1949), 442–453.Google Scholar
(6) Etherington, I. M. H., Theory of indices for non-associative algebra, Proc. Roy. Soc. Edinburgh Sect. A 64 (1955), 150–160.Google Scholar
(7) Etherington, I. M. H. and Erdelyi, A., Some problems of non-associative combinations (2), Edin. Math. Notes 32 (1941), 7–12.Google Scholar
(8) Evans, Trevor, Non-associative number theory, Amer. Math. Monthly 64 (1957), 299–309.Google Scholar
(9) Robinson, A., On non-associative systems, Proc. Edinburgh Math. Soc. (2) 8 (1949), 111–118.Google Scholar
(10) Minc, H., Theorems on non-associative number theory, Amer. Math. Monthly 66 (1959), 486–488.Google Scholar