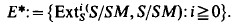Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-26T01:09:45.324Z Has data issue: false hasContentIssue false
  • English
  • Français

Cohomology of induced modules in rings of differential operators

Published online by Cambridge University Press:  20 January 2009

Kenneth A. Brown  and
Thierry Levasseur
Kenneth A. Brown
Affiliation:
Department of MathematicsUniversity of GlasgowGlasgow G11 5HF, Scotland
Thierry Levasseur
Affiliation:
Departement de MathématiquesUniversité de Paris VITour 45-46-5e4 place JussieuParis, France
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let K be a field of characteristic zero and let Δ ={δ1,…,δn} be a set of commuting K-derivations of the commutative Noetherian K-algebra R. Let S = R[X1,…,Xn] be the corresponding ring of differential operators, so [Xi, r] = Xir − rXi=δi(r and [Xi, Xj]=0, for 1≦i, j≦n. Let M be a maximal ideal of R with R/M of finite dimension over K. The purpose of this note is to describe the groups

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 31 , Issue 1 , February 1988 , pp. 41 - 47
Copyright
Copyright © Edinburgh Mathematical Society 1988

References

REFERENCES

1.Bourbaki, N., Algèbre Commutative, Chapter X (Massen, Paris, 1983).Google Scholar
2.Bjork, J.-E., Rings of Differential Operators (North-Holland, Amsterdam, 1979).Google Scholar
3.Goodearl, K. and Lenegan, T. H., Krull dimension of differential operator rings IV—multiple derivations, Proc. London Math. Soc. (3) 47 (1983), 306–336.CrossRefGoogle Scholar
4.Lipman, J., Free derivation modules on algebraic varieties, Amer. J. Math. 87 (1965), 874–898.CrossRefGoogle Scholar
5.Rotman, J., An Introduction to Homological Algebra (Academic Press, New York, 1979).Google Scholar
6.Zariski, O. and Samuel, P., Commutative Algebra, Volume II (Van Nostrand, Princeton, 1960).CrossRefGoogle Scholar