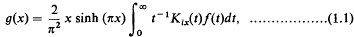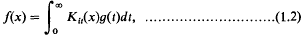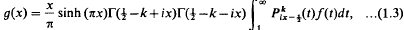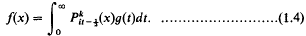Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
1969.
The Special Functions and their Approximations.
Vol. 53,
Issue. ,
p.
453.
1969.
The Special Functions and Their Approximations.
Vol. 53,
Issue. ,
p.
330.
Mielke, Eckehard W.
1977.
Quantenfeldtheorie im de Sitter‐Raum.
Fortschritte der Physik,
Vol. 25,
Issue. 1-12,
p.
401.
1985.
Transmutation Theory and Applications.
Vol. 117,
Issue. ,
p.
323.
Pathak, R. S.
and
Mishra, S. K.
1989.
Asymptotic behaviours of a class of integral transforms in complex domains.
Proceedings of the Edinburgh Mathematical Society,
Vol. 32,
Issue. 2,
p.
231.
Denzler, Jochen
1997.
A hypergeometric function approach to the persistence problem of single sine-Gordon breathers.
Transactions of the American Mathematical Society,
Vol. 349,
Issue. 10,
p.
4053.
Pathak, R.S.
1999.
Integral transforms and asymptotics of generalized functions.
Integral Transforms and Special Functions,
Vol. 8,
Issue. 1-2,
p.
105.
Hazewinkel, Michiel
2000.
Encyclopaedia of Mathematics.
p.
271.
Yarotskaya, L.D.
2000.
On index transforms with meijer'sG-function kernels.
Integral Transforms and Special Functions,
Vol. 10,
Issue. 3-4,
p.
309.
Yakubovich, S.B.
2000.
The Titchmarsh integral transformation by the index of a Bessel function.
Journal of Computational and Applied Mathematics,
Vol. 118,
Issue. 1-2,
p.
353.
Gasaneo, G
and
Colavecchia, F D
2003.
Two-body Coulomb wavefunctions as kernel for alternative integral transformations.
Journal of Physics A: Mathematical and General,
Vol. 36,
Issue. 31,
p.
8443.
Szmytkowski, Radosław
and
Bielski, Sebastian
2010.
An orthogonality relation for the Whittaker functions of the second kind of imaginary order.
Integral Transforms and Special Functions,
Vol. 21,
Issue. 10,
p.
739.
Hong, Nguyen Thanh
Tuan, Trinh
and
Thao, Nguyen Xuan
2013.
On the Fourier cosine-Kontorovich-Lebedev generalized convolution transforms.
Applications of Mathematics,
Vol. 58,
Issue. 4,
p.
473.
2013.
The Kontorovich–Lebedev Transform as a Map between d‐Orthogonal Polynomials.
Studies in Applied Mathematics,
Vol. 131,
Issue. 3,
p.
229.
Zuparic, Mathew
2015.
On polynomial solutions to Fokker–Planck and sinked density evolution equations.
Journal of Physics A: Mathematical and Theoretical,
Vol. 48,
Issue. 13,
p.
135202.
Blower, Gordon
and
Chen, Yang
2016.
Kernels and point processes associated with Whittaker functions.
Journal of Mathematical Physics,
Vol. 57,
Issue. 9,
Khoa, Nguyen Minh
Hong, Nguyen Thanh
and
Tuan, Vu Kim
2017.
On Fourier – Kontorovich–Lebedev generalized convolution transforms.
Integral Transforms and Special Functions,
Vol. 28,
Issue. 4,
p.
271.
Sousa, Rúben
Guerra, Manuel
and
Yakubovich, Semyon
2019.
On the product formula and convolution associated with the index Whittaker transform.
Journal of Mathematical Analysis and Applications,
Vol. 475,
Issue. 1,
p.
939.
Tuan, T.
2020.
On the Fourier-Sine and Kontorovich–Lebedev Generalized Convolution Transforms and Their Applications.
Ukrainian Mathematical Journal,
Vol. 72,
Issue. 2,
p.
302.
Yakubovich, Semyon
2021.
Discrete Index Whittaker Transforms.
Results in Mathematics,
Vol. 76,
Issue. 2,