Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Perets, Gadi S.
and
Polo, Patrick
1995.
On the Hattori-Stallings trace for certain primitive factors of enveloping algebras of semisimple Lie algebras.
Mathematische Zeitschrift,
Vol. 219,
Issue. 1,
p.
227.
Holland, Martin P.
and
Polo, Patrick
1996.
K-theory of twisted differential operators on flag varieties.
Inventiones Mathematicae,
Vol. 123,
Issue. 1,
p.
377.


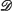 -modules on the flag variety
-modules on the flag variety )→ℤ, where
)→ℤ, where 