Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-12-01T03:18:25.080Z Has data issue: false hasContentIssue false
  • English
  • Français

Characterizations of linear differential systems with a regular singular point

Published online by Cambridge University Press:  20 January 2009

W. A. Harris Jr.
W. A. Harris Jr.
Affiliation:
University of Southern California, Los Angeles, California
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The linear differential system

where w is a vector with n components and A is an n by n matrix is said to have z = 0 as a regular singular point if there exists a fundamental matrix of the form

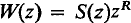
such that S is holomorphic at z = 0 and R is a constant matrix ((1), p. 111; (2), p. 73). For such systems A will have at most a pole at z = 0 and we may write

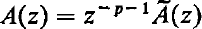
where p is an integer, Ã is holomorphic at z = 0, and Ã(0) ≠ 0. However, the converse is not true. When p ≦ − 1, A is holomorphic at z = 0, and every fundamental matrix is holomorphic at z = 0. If p ≧ 1, the non-negative integer p is called (after Poincaré) the rank of the singularity and there is a significant difference between the cases p = 0 and p ≧ 1. If p = 0 the linear differential system (1) is known to have z = 0 as a regular singular point ((1), p. 111) ; whereas, if p ≧ 1, z = 0 may or may not be a regular singular point.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 18 , Issue 2 , December 1972 , pp. 93 - 98
Copyright
Copyright © Edinburgh Mathematical Society 1972

References

REFERENCES

(1) Coddington, E. A. and Levinson, N., Theory of Ordinary Differential Equations (McGraw-Hill, New York, 1955).Google Scholar
(2) Hartman, P., Ordinary Differential Equations (Wiley, New York, 1964).Google Scholar
(3) Jurkat, W. B. and Lutz, D. A., On the order of solutions of analytic differential equations, Proc. London Math. Soc. 22 (1971), 465–482.CrossRefGoogle Scholar
(4) Lutz, D. A., Some characterizations of systems of linear differential equations having regular singular solutions, Trans. Amer. Math. Soc. 126 (1967), 427–441.CrossRefGoogle Scholar
(5) Lutz, D. A., On systems of linear differential equations having regular singular solutions, J. of Differential Equations 3 (1967), 311–322.CrossRefGoogle Scholar
(6) Lutz, D. A., On the reduction of rank of linear differential system, Pacific J. Math. To appear.Google Scholar
(7) Moser, J., The order of a singularity in Fuchs' theory, Math. Z. 72 (1960), 379–398.CrossRefGoogle Scholar
(8) TuRRrrnN, H. L., Reducing the rank of ordinary differential equations, Duke Math. J. 30 (1963), 271–274.Google Scholar
(9) Wasow, W., Simplification of turning point problems for systems of linear differential equations, Trans. Amer. Math. Soc. 106(1963), 100–114.CrossRefGoogle Scholar