No CrossRef data available.
Published online by Cambridge University Press: 03 October 2024
In this paper, we consider blowup of solutions to the Cauchy problem for the following biharmonic nonlinear Schrödinger equation (NLS),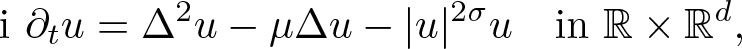 \begin{equation*}\text{i } \partial_t u=\Delta^2 u-\mu \Delta u-|u|^{2 \sigma} u \quad \text{in} \,\, \mathbb{R} \times \mathbb{R}^d,\end{equation*}
\begin{equation*}\text{i } \partial_t u=\Delta^2 u-\mu \Delta u-|u|^{2 \sigma} u \quad \text{in} \,\, \mathbb{R} \times \mathbb{R}^d,\end{equation*}
where 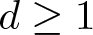 $d \geq 1$,
$d \geq 1$, 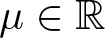 $\mu \in \mathbb{R}$ and
$\mu \in \mathbb{R}$ and 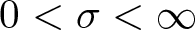 $0 \lt \sigma \lt \infty$ if
$0 \lt \sigma \lt \infty$ if 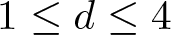 $1 \leq d \leq 4$ and
$1 \leq d \leq 4$ and 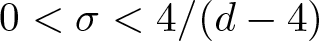 $0 \lt \sigma \lt 4/(d-4)$ if
$0 \lt \sigma \lt 4/(d-4)$ if 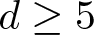 $d \geq 5$. In the mass critical and supercritical cases, we establish the existence of blowup solutions to the problem for cylindrically symmetric data. The result extends the known ones with respect to blowup of solutions to the problem for radially symmetric data.
$d \geq 5$. In the mass critical and supercritical cases, we establish the existence of blowup solutions to the problem for cylindrically symmetric data. The result extends the known ones with respect to blowup of solutions to the problem for radially symmetric data.