In this paper we generalise some of the results obtained in [1] for the n-dimensional real spaces ℓp(n) to the infinite dimensional real spaces ℓp. Let p >1 with p ≠ 2, and let x be a non-zero real sequence in ℓp. Let ε(x) denote the closed linear subspace spanned by the set 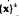of all those sequences in ℓp which are biorthogonal to x with respect to the unique semi-inner-product on ℓp consistent with the norm on ℓp. In this paper we show that codim ε(x)=1 unless either x has exactly two non-zero coordinates which are equal in modulus, or x has exactly three non-zero coordinates α, β, γ with |α| ≥ |β| ≥ |γ| and |α|p > |β|p + |γ|p. In these exceptional cases codim ε(x) = 2. We show that 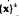is a linear subspace if, and only if, x has either at most two non-zero coordinates or x has exactly three non-zero coordinates which satisfy the inequalities stated above.