Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-24T00:54:07.529Z Has data issue: false hasContentIssue false
  • English
  • Français

Bilattices and Morita Equivalence of MASA Bimodules

Part of: Linear spaces and algebras of operators

Published online by Cambridge University Press:  20 November 2015

G. K. Eleftherakis
G. K. Eleftherakis*
Affiliation:
University of Patras, Faculty of Sciences, Department of Mathematics, 265 00 Patras, Greece ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

We define an equivalence relation between bimodules over maximal abelian self-adjoint algebras (MASA bimodules), which we call spatial Morita equivalence. We prove that two reflexive MASA bimodules are spatially Morita equivalent if and only if their (essential) bilattices are isomorphic. We also prove that if 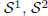are bilattices that correspond to reflexive MASA bimodules 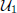, 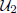and 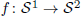is an onto bilattice homomorphism, then

(i) if 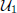is synthetic, then 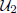is synthetic;

(ii) if 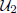contains a non-zero compact (or a finite or a rank 1) operator, then 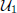also contains a non-zero compact (or a finite or a rank 1) operator.

Keywords

MASA bimodulesMorita equivalencereflexivity

MSC classification

Secondary: 47L35: Nest algebras, CSL algebras 47L05: Linear spaces of operators
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 59 , Issue 3 , August 2016 , pp. 605 - 621
Copyright
Copyright © Edinburgh Mathematical Society 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Arveson, W. B., Operator algebras and invariant subspaces, Annals Math. 100(2) (1974), 433–532.CrossRefGoogle Scholar
2. Davidson, K. R., Nest algebras (Longman, New York, 1988).Google Scholar
3. Edwards, D. A., Some characterizations of commutative subspace lattices, Bull. Lond. Math. Soc. 36(2) (2004), 252–262.Google Scholar
4. Eleftherakis, G. K., TRO equivalent algebras, Houston J. Math. 38(1) (2012), 153–175.Google Scholar
5. Eleftherakis, G. K., Applications of operator space theory to nest algebra bimodules, Integ. Eqns Operat. Theory 72(4) (2012), 577–595.Google Scholar
6. Eleftherakis, G. K., Paulsen, V. I. and Todorov, I. G., Stable isomorphism of dual operator spaces, J. Funct. Analysis 258 (2010), 260–278.Google Scholar
7. Erdos, J. A., Reflexivity for subspace maps and linear spaces of operators, Proc. Lond. Math. Soc. 52(3) (1986), 582–600.Google Scholar
8. Erdos, J. A., Katavolos, A. and Shulman, V. S., Rank one subspaces of bimodules over maximal abelian self-adjoint algebras, J. Funct. Analysis 157(2) (1998), 554–587.Google Scholar
9. Loginov, A. I. and Shulman, V. S., Hereditary and intermediate reflexivity of W*-algebras, Izv. Akad. Nauk SSSR 39 (1975), 1260–1273.Google Scholar
10. Shulman, V. S. and Turowska, L., Operator synthesis, I, Synthetic sets, bilattices and tensor algebras, J. Funct. Analysis 209 (2004), 293–331.Google Scholar
11. Shulman, V. S., Todorov, I. G. and Turowska, L., Sets of multiplicity and closable multipliers on group algebras, J. Funct. Analysis 268(6) (2014), 1454–1508.Google Scholar