Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-28T07:02:31.285Z Has data issue: false hasContentIssue false
  • English
  • Français

Averaging the sum of digits function to an even base

Published online by Cambridge University Press:  20 January 2009

D. M. E. Foster
D. M. E. Foster
Affiliation:
Mathematical InstituteUniversity of St AndrewsNorth HaughSt Andrews KY16 9SS
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For a fixed integer q≧2, every positive integer 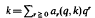where each ar(q, k) ∈ {0, 1, 2, …, q–1}. The sum of digits function α(q, k) = 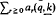behaves rather erratically but on averaging has a uniform behaviour. In particular if A(q, n) = 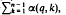, where n > 1, then it is well known that A(q, n)∼½ ((q – 1)/log q) n log n as n→∞. For even values of q, a lower bound is now given for the difference ½S(q, n) = A(q, n)–½(q–1)[logn/logq] n, where [log n/log q] denotes the greatest integer ≦ log n/log q, complementing an earlier result for odd values of q.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 35 , Issue 3 , October 1992 , pp. 449 - 455
Copyright
Copyright © Edinburgh Mathematical Society 1992

References

REFERENCES

1.Bush, L. E., An asymptotic formula for the average sums of the digits of integers, Amer Math. Monthly 47 (1940), 154–156.CrossRefGoogle Scholar
2.Foster, D. M. E., Estimates for a remainder term associated with the sum of digits function, Glasgow Math. J. 29 (1987), 109–129.CrossRefGoogle Scholar
3.Foster, D. M. E., A lower bound for a remainder term associated with the sum of digits function, Proc. Edinburgh Math. Soc. 34 (1991), 121–142.CrossRefGoogle Scholar
4.Stolarsky, K. B., Power and exponential sums of digital sums related to binomial coefficient parity, SIAM J. Appl. Math. 32 (1977), 717–730.CrossRefGoogle Scholar