Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-12-01T00:00:51.010Z Has data issue: false hasContentIssue false
  • English
  • Français

Asymptotic Representation of Certain Real Integrals with Parameter-dependent Limits of Integration

Published online by Cambridge University Press:  20 January 2009

E. W. Ross Jr
E. W. Ross Jr
Affiliation:
Watertown Arsenal, Watertown, Mass., U.S.A. and King's College, Newcastle-upon-Tyne
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we consider a function f(x) defined by

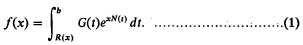
All quantities are taken to be real, it is assumed that R is a function of the variable x, b is a constant, N and G are functions of the variable t and all the functions are such that the integral (1) exists when x is large enough. We wish to find an asymptotic representation of f(x) as x → + ∞, assuming that we are given certain information about the limiting behaviours of the functions R, N and G.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 12 , Issue 4 , December 1961 , pp. 177 - 187
Copyright
Copyright © Edinburgh Mathematical Society 1961

References

REFERENCES

(1) ErdÉlyi, A., Asymptotic Expansions (New York, Dover Publication, 1956), p. 37 ff.Google Scholar
(2) Bateman Manuscript Project, Higher Transcendental Functions, Volume II (New York, McGraw-Hill, 1953), pp. 133–145Google Scholar