Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-07T10:30:13.429Z Has data issue: false hasContentIssue false
  • English
  • Français

Asymptotic Expressions for the Bessel Functions and the Fourier-Bessel Expansions

Published online by Cambridge University Press:  20 January 2009

T. M. MacRobert
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Asymptotic Expressions for the Bessel Functions.

From the asymptotic expansion for Ku(z) it follows that, if − π < amp z < π,

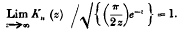
This theorem is also true if amp z = ± π; to prove this consider the formula

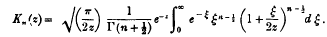
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 39 , February 1920 , pp. 13 - 20
Copyright
Copyright © Edinburgh Mathematical Society 1920

References

* This will be clear if N and M tend to infinity together in such a way that the line joining the origin to the point M + i N makes a finite angle with the imaginary axis; for instance, if M = N.

* When n is not an integer the integral along the ε-axis becomes