Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-26T00:44:57.902Z Has data issue: false hasContentIssue false
  • English
  • Français

Asymptotic expansion of a series of Ramanujan

Published online by Cambridge University Press:  20 January 2009

Bruce C. Berndt  and
Ronald J. Evans
Bruce C. Berndt
Affiliation:
Department of Mathematics1409 West Green StreetUniversity of IllinoisUrbana, IL 61801
Ronald J. Evans
Affiliation:
Department of MathematicsUniversity of California, San DiegoLa Jolla, CA 92093–0112
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

An asymptotic expansion is given for the series

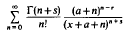
as x→∞ in the sector |Argx|≦π/2–δ. Here δ, Re(a), and Re(s) are positive and r is a positive integer. In the case a = r = s = 1, this yields the nontrivial result

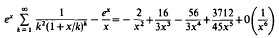
stated by Ramanujan in his notebooks [6].

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 35 , Issue 2 , June 1992 , pp. 189 - 199
Copyright
Copyright © Edinburgh Mathematical Society 1992

References

REFERENCES

1.Abramowitz, M. and Stegun, I., Handbook of Mathematical Functions (Dover, New York, 1972).Google Scholar
2.Berndt, B. C., Ramanujan's Notebooks, Part V (Springer-Verlag, New York), to appear.Google Scholar
3.Erdélyi, A., ed., Higher Transcendental Functions, Vol. II (McGraw-Hill, New York, 1953).Google Scholar
4.Lebedev, N. N., Special Functions and their Applications (Dover, New York, 1972).Google Scholar
5.Olver, F. W. J., Asymptotics and Special Functions (Academic Press, New York, 1974).Google Scholar
6.Ramanujan, S., Notebooks (2 volumes) (Tata Institute of Fundamental Research, Bombay, 1957).Google Scholar
7.Riordan, J., An Introduction to Combinatorial Analysis (Princeton University Press, Princeton, New Jersey, 1978).Google Scholar
8.Roman, S., The formula of Faa di Bruno, Amer. Math. Monthly 87 (1980), 805–809.CrossRefGoogle Scholar