Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-26T01:06:11.739Z Has data issue: false hasContentIssue false
  • English
  • Français

Asymptotic behaviour of ideals relative to injective modules over commutative Noetherian rings II

Published online by Cambridge University Press:  20 January 2009

H. Ansari Toroghy  and
R. Y. Sharp
H. Ansari Toroghy
Affiliation:
Department of Pure MathematicsUniversity of SheffieldHicks BuildingSheffield S3 7RH
R. Y. Sharp
Affiliation:
Department of Pure MathematicsUniversity of SheffieldHicks BuildingSheffield S3 7RH
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let E be an injective module over a commutative Noetherian ring A (with non-zero identity), and let a be an ideal of A. The submodule (0:Eα) of E has a secondary representation, and so we can form the finite set AttA(0:Eα) of its attached prime ideals. In [1, 3.1], we showed that the sequence of sets 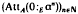is ultimately constant; in [2], we introduced the integral closure a*(E) of α relative to E, and showed that 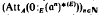is increasing and ultimately constant. In this paper, we prove that, if a contains an element r such that rE = E, then 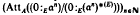is ultimately constant, and we obtain information about its ultimate constant value.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 35 , Issue 3 , October 1992 , pp. 511 - 518
Copyright
Copyright © Edinburgh Mathematical Society 1992

References

REFERENCES

1.Toroghy, H. Ansari and Sharp, R. Y., Asymptotic behaviour of ideals relative to injective modules over commutative Noetherian rings, Proc. Edinburgh Math. Soc. (2) 34 (1991), 155–160.Google Scholar
2.Toroghy, H. Ansari and Sharp, R. Y., Integral closures of ideals relative to injective modules over commutative Noetherian rings, Oxford Quart. J. Math. (2) 42 (1991), 393–402.CrossRefGoogle Scholar
3.Brodmann, M., Asymptotic stability of Ass(M/InM), Proc. Amer. Math. Soc. 74 (1979), 16–18.Google Scholar
4.Kirby, D., Coprimary decomposition of Artinian modules, J. London Math. Soc. (2) 6 (1973), 571–576.Google Scholar
5.Macdonald, I. G., Secondary representation of modules over a commutative ring, in Symposia Matematica 11 (Istituto Nazionale di alta Matematica, Roma, 1973), 23–43.Google Scholar
6.Matlis, E., Injective modules over Noetherian rings, Pacific J. Math. 8 (1958), 511–528.Google Scholar
7.McAdam, S., Asymptotic prime divisors (Lecture Notes in Mathematics 1023, Springer, Berlin, 1983).Google Scholar
8.Northcott, D. G., Generalized Koszul complexes and Artinian modules, Quart. J. Math. Oxford (2) 23 (1972), 289–297.CrossRefGoogle Scholar
9.Northcott, D. G. and Rees, D., Reductions of ideals in local rings, Proc. Cambridge Philos. Soc. 50 (1954), 145–158.Google Scholar
10.Ratliff, L. J. Jr., On asymptotic prime divisors, Pacific J. Math. 111 (1984), 395–413.CrossRefGoogle Scholar
11.Sharp, R. Y., The Cousin complex for a module over a commutative Noetherian ring, Math. Z. 112 (1969), 340–356.CrossRefGoogle Scholar
12.Sharp, R. Y., Secondary representations for injective modules over commutative Noetherian rings, Proc. Edinburgh Math. Soc. (2) 20 (1976), 143–151.CrossRefGoogle Scholar
13.Sharp, R. Y., Asymptotic behaviour of certain sets of attached prime ideals, J. London Math. Soc. (2) 34 (1986), 212–218.Google Scholar
14.Sharpe, D. W. and Vámos, P., Injective modules (Cambridge University Press, 1972).Google Scholar