No CrossRef data available.
Published online by Cambridge University Press: 20 January 2009
The initial-boundary value problem for the nonlinear heat equation u1 = Δu + λf(u) might possibly have global classical unbounded solutions, for some “critical” initial data 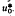 . The asymptotic behaviour of such solutions is studied, when there exists a unique bounded steady state w(x;λ) for some values of λ We find, for radial symmetric solutions, that u*(r, t)→w(r) for any 0<r≤l but supu*(·, t) = u*(0, t)→∞, as t→∞. Furthermore, if
. The asymptotic behaviour of such solutions is studied, when there exists a unique bounded steady state w(x;λ) for some values of λ We find, for radial symmetric solutions, that u*(r, t)→w(r) for any 0<r≤l but supu*(·, t) = u*(0, t)→∞, as t→∞. Furthermore, if 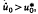 , where
, where 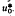 is some such critical initial data, then û = u(x, t; û0) blows up in finite time provided that f grows sufficiently fast.
is some such critical initial data, then û = u(x, t; û0) blows up in finite time provided that f grows sufficiently fast.