Dr E. M. Horsburgh has given the approximate expression for the length of an arc of the catenary:

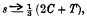
where C is the length of the chord and T the sum of the tangents at its extremities, analogous to Huygens' approximation to the length of a circular arc:

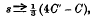
where C′ is the sum of the chords of the two halves of the arc. These approximations are not confined to these particular curves, but hold, within wider or narrower limits, for any continuous curve. In fact, if s is regarded as a small quantity of the first order, as are also C, C′ and T, the difference between s and either of the quantities ⅓(2C + T) and ⅓(4C″ – C) is a small quantity of the fifth order. Other expressions of a similar form can be found involving the chords and tangents of the half-arcs.