Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-25T14:09:40.076Z Has data issue: false hasContentIssue false
  • English
  • Français

Approximation numbers of composition operators on weighted besov spaces of analytic functions

Part of: Special classes of linear operators Two-dimensional theory Spaces and algebras of analytic functions

Published online by Cambridge University Press:  28 February 2022

Stamatis Pouliasis
Stamatis Pouliasis*
Affiliation:
Department of Mathematics and Statistics, Texas Tech University, Lubbock, TX 79409, USA ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

Li et al. [A spectral radius type formula for approximation numbers of composition operators, J. Funct. Anal. 267(12) (2014), 4753-4774] proved a spectral radius type formula for the approximation numbers of composition operators on analytic Hilbert spaces with radial weights and on $H^{p}$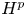 spaces, $p\geq 1$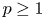, involving Green capacity. We prove that their formula holds for a wide class of Banach spaces of analytic functions and weights.

Keywords

composition operatorsapproximation numbersBesov spacescondenser capacityBagby points

MSC classification

Primary: 47B06: Riesz operators; eigenvalue distributions; approximation numbers, $s$-numbers, Kolmogorov numbers, entropy numbers, etc. of operators 47B33: Composition operators
Secondary: 30H25: Besov spaces and $Q_p$-spaces 31A15: Potentials and capacity, harmonic measure, extremal length
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 65 , Issue 2 , May 2022 , pp. 311 - 325
Check for updates
Copyright
Copyright © The Author(s), 2022. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aleman, A., The multiplication operator on Hilbert spaces of analytic functions, (Habilitation, FernUniversität Hagen, 1993).Google Scholar
Bagby, T., The modulus of a plane condenser, J. Math. Mech. 17 (1967), 315–329.Google Scholar
Bao, G., Göğüş, N. G. and Pouliasis, S., On Dirichlet spaces with a class of superharmonic weights, Canad. J. Math. 70 (2018), 721–741.CrossRefGoogle Scholar
Costara, C. and Ransford, T., Which de Branges-Rovnyak spaces are Dirichlet spaces (and vice versa)?, J. Funct. Anal. 265 (2013), 3204–3218.CrossRefGoogle Scholar
Cowen, C. C. and MacCluer, B. D., Composition operators on spaces of analytic functions, Studies in Advanced Mathematics (CRC Press, 1995).Google Scholar
Dubinin, V. N., Condenser capacities and symmetrization in geometric function theory, Translated from the Russian by Nikolai G. Kruzhilin (Springer, Basel, 2014).CrossRefGoogle Scholar
El-Fallah, O., Kellay, K., Mashreghi, J. and Ransford, T., A primer on the Dirichlet space, Cambridge Tracts in Mathematics, Volume 203 (Cambridge University Press, 2014).CrossRefGoogle Scholar
El-Fallah, O., Kellay, K., Klaja, H., Mashreghi, J. and Ransford, T., Dirichlet spaces with superharmonic weights and de Branges-Rovnyak spaces, Complex Anal. Operator Theory 10 (2016), 97–107.CrossRefGoogle Scholar
Fisher, S. D., Function theory on planar domains. A second course in complex analysis, Pure and Applied Mathematics (John Wiley and Sons, 1983).Google Scholar
Götz, M., Approximating the condenser equilibrium distribution, Math. Z. 236(4) (2001), 699–715.CrossRefGoogle Scholar
Kloke, H., Punktsysteme mit extremalen Eigenschaften für ebene Kondensatoren, Dissertation Universität Dortmund, 1984.Google Scholar
Kloke, H., On the capacity of a plane condenser and conformal mapping, J. Reine Angew. Math. 358 (1985), 179–201.Google Scholar
Landkof, N. S., Foundations of Modern Potential Theory (Springer-Verlag, 1972).CrossRefGoogle Scholar
Li, D., Queffélec, H. and Rodríguez-Piazza, L., A spectral radius type formula for approximation numbers of composition operators, J. Funct. Anal. 267(12) (2014), 4753–4774.CrossRefGoogle Scholar
Richter, S., A representation theorem for cyclic analytic two-isometries, Trans. Amer. Math. Soc. 328 (1991), 325–349.CrossRefGoogle Scholar
Richter, S. and Sundberg, C., A formula for the local Dirichlet integral, Michigan Math. J. 38 (1991), 355–379.CrossRefGoogle Scholar
Sarason, D., Local Dirichlet spaces as de Branges-Rovnyak spaces, Proc. Amer. Math. Soc. 125 (1997), 2133–2139.CrossRefGoogle Scholar
Shapiro, J. H., Composition operators and classical function theory, Universitext, Tracts in Mathematics (Springer-Verlag, 1993).CrossRefGoogle Scholar
Shimorin, S. M., Complete Nevanlinna-Pick property of Dirichlet-type spaces, J. Funct. Anal. 191 (2002), 276–296.CrossRefGoogle Scholar
Siciak, J., Wiener's type regularity criteria on the complex plane, Ann. Polon. Math. 66 (1997), 203–221.CrossRefGoogle Scholar
Vuorinen, M., Conformal geometry and quasiregular mappings, Lecture Notes in Math. Volume 1319 (Springler-Verlag, 1988).CrossRefGoogle Scholar
Widom, H., Rational approximation and $n$-dimensional diameter, J. Approx. Theory 5 (1972), 343–361.CrossRefGoogle Scholar
Wojtaszczyk, P., Banach spaces for analysts, Cambridge Studies in Advanced Mathematics, Volume 25 (Cambridge University Press, 1991).CrossRefGoogle Scholar
Zhu, K., Operator theory in function spaces, 2nd edn, Mathematical Surveys and Monographs, Volume 138 (American Mathematical Society, 2007).CrossRefGoogle Scholar