Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-05T21:29:55.306Z Has data issue: false hasContentIssue false
  • English
  • Français

Approximation and spectral properties of periodic spline operators

Published online by Cambridge University Press:  20 January 2009

S. L. Lee  and
W. S. Tang
S. L. Lee
Affiliation:
Department of MathematicsNational University of Singapore10 Kent Ridge CrescentSingapore 0511
W. S. Tang
Affiliation:
Department of MathematicsNational University of Singapore10 Kent Ridge CrescentSingapore 0511
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We consider discrete convolution operators 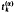whose range is the k-dimensional space 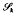spanned by the translates of a single function. Examples of 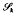include the space of trigonometric polynomials, periodic polynomial splines and trigonometric splines. The eigenfunctions of these operators corresponding to the nonzero eigenvalues are independent of α, and they form an orthogonal basis for 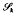. The limiting behaviour of 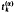as α, k→∞, is also considered. The corresponding limiting semigroups are computed explicitly.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 34 , Issue 3 , October 1991 , pp. 363 - 382
Copyright
Copyright © Edinburgh Mathematical Society 1991

References

REFERENCES

1.Berens, H., Interpolationsmethoden zur Behandlung von Approximationsprozessen auf Banach-räumen (Lecture Notes in Math. 64, Springer 1968).CrossRefGoogle Scholar
2.Butzer, P. L. and Berens, H., Semi-Groups of Operators and Approximation (Springer-Verlag 1967).CrossRefGoogle Scholar
3.Butzer, P. L. and Nessel, R. J., Fourier Analysis and Approximation, Vol. 1 (Academic Press 1971).CrossRefGoogle Scholar
4.Davis, P. J., Circulant Matrices (Wiley 1979).Google Scholar
5.Delvos, Franz-Jürgen, Periodic interpolation on uniform meshes, J. Approx. Theory 51 (1987), 71–80.CrossRefGoogle Scholar
6.Goodman, T. N. T. and Lee, S. L., B-splines on the circle and trigonometric B-splines, Proc. Conf. on Approx. Theory and spline functions (Singh, S. P., Bury, J. W. H. and Watson, B., eds., St. Johns, Newfoundland, Reidel Pub. Co., 1983), 297–325.Google Scholar
7.Goodman, T. N. T. and Lee, S. L., Convolution operators with trigonometric spline kernels, Proc. Edinburgh Math. Soc. 31 (1988), 285–299.CrossRefGoogle Scholar
8.Kamada, Masaru, Toraichi, Kazuo and Mori, Ryoichi, Periodic spline orthonormal bases, J. Approx. Theory 55 (1988), 27–34.CrossRefGoogle Scholar
9.Karlin, S. and Zeigler, Z., Iteration of positive approximation operators, J. Approx. Theory 3 (1970), 310–399.CrossRefGoogle Scholar
10.Korovkin, P. P., Linear Operators and Approximation Theory (Hindustan Publ. 1960).Google Scholar
11.Locher, F., Interpolation on uniform meshes by translates of one function and related attenuation factors, Math. Comp. 37 (1981), 403–416.CrossRefGoogle Scholar
12.Marsden, M. J., An identity for spline functions with applications to variation diminishing spline approximation, J. Approx. Theory 3 (1970), 7–49.CrossRefGoogle Scholar
13.Meinardus, G., Periodische splinefunktionen, in Spline functions, Karlsruhe 1975 (Bohner, K., Meinardus, G. and Schempp, W., eds., Lecture Notes in Math. 501, Springer 1976).Google Scholar
14.Polya, G. and Schoenberg, I. J., Remarks on de la Vallée Poussin means and convex conformal maps on the circle, Pacific J. Math. 8 (1958), 295–334.CrossRefGoogle Scholar
15.Schoenberg, I. J., On interpolation by spline functions and its minimal properties, in On Approximation Theory (Intern. Ser. Numerical Math (ISNM), Birkhauser 5, 1964), 109–129.Google Scholar
16.Schoenberg, I. J., On trigonometric spline interpolation, J. Math. Mech. 13 (1964), 795–825.Google Scholar
17.Schoenberg, I. J., On polynomial splines on the circle I, in Proc. Conf. on Constructive Theory of Functions (Budapest 1972), 403–433.Google Scholar