Hostname: page-component-f554764f5-nt87m Total loading time: 0 Render date: 2025-04-11T09:51:51.983Z Has data issue: false hasContentIssue false
  • English
  • Français

Approximation and interpolation by complex splines on the torus

Published online by Cambridge University Press:  20 January 2009

T. N. T. Goodman ,
S. L. Lee  and
A. Sharma
T. N. T. Goodman
Affiliation:
Department of Mathematical and Computing Sciences, University of Dundee, Dundee DD1 4HN, Scotland
S. L. Lee
Affiliation:
School of Mathematical and Computer Sciences, Science University of Malaysia, Penang 11800, Malaysia and Department of Mathematics, National University of Singapore, 10 Kent Crescent, Singapore 0511
A. Sharma
Affiliation:
Department of Mathematics, University of Alberta, Edmonton, Alberta T6G 2G1, Canada
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let T2 = {(eix1, eix2):0 ≦ xj<2π, j=1,2} be a two dimensional torus and r, s, t and k be positive integers with k>r+s+t–2. Our main object is to study the approximation and interpolation properties of a class of smooth functions whose restrictions to each triangle of a three direction mesh lie in the linear span of 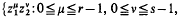or 0≦μ≦r–1, r+s–l≦μ+ν≦r+s+t–2, or 0≦ν≦s–1, r+s–1≦μ+ν≦r+s+t–2} Where (z1, z2) ∈ T2.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 32 , Issue 2 , June 1989 , pp. 197 - 212
Copyright
Copyright © Edinburgh Mathematical Society 1989

References

REFERENCES

1.Ahlberg, J. H., Nilson, E. N. and Walsh, J. L., Properties of analytic splines I: Complex polynomial splines, J. Analysis and Appl. 33 (1971), 234–257.Google Scholar
2.De Boor, C., Hollig, K. and Riemenschneider, S. D., Bivariate cardinal interpolation by splines on a three direction mesh, Illinois J. Math. 29 (1985), 555–566.CrossRefGoogle Scholar
3.Dahmen, W. and Micchelli, C. A., On limits of multivariate B-splines, J. Analyse Math. 39 (1981), 256–278.Google Scholar
4.Dahmen, W. and Micchelli, C. A., On the local linear independence of translates of a box spline, Stud. Math. Appl. 82 (1985), 243–263.Google Scholar
5.Goodman, T. N. T. and Lee, S. L., B-splines on the circle and trigonometric B-splines, Proc. Conference on Approx. Theory, St. John's, Newfoundland (Reidel Pub. Co., 1983), 297–325.Google Scholar
6.Hollig, K., Box splines, Approximation Theory V (Academic Press, Boston, Mass., 1986), 71–95.Google Scholar
7.Jia, R. Q., On the linear independence of translates of box splines, J. Approx. Theory 40 (1984), 158–160.CrossRefGoogle Scholar
8.Micchelli, C. A. and Sharma, A., Spline functions on the circle: Cardinal L-splines revisited, Canad. J. Math. 32 (1980), 1459–1473.CrossRefGoogle Scholar
9.Ron, Amos, Exponential box splines, to appear in Constructive Approximation.Google Scholar
10.Schoenberg, I. J., On polynomial spline functions on the circle I and II, Proc. Conference on Constructive Theory of Functions, Budapest (1972), 403–433.Google Scholar