Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-20T02:20:44.175Z Has data issue: false hasContentIssue false
  • English
  • Français

An upper bound for λ1 for Γ(q) and Γ0(q)

Published online by Cambridge University Press:  20 January 2009

C. J. Mozzochi
C. J. Mozzochi
Affiliation:
P.O. Box 1424, Princeton, NJ 08542, USA
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Under the assumption of the Selberg conjecture I establish by means of the Selberg trace formula the following:

Theorem. Let Γ denote Γ(q) or Γ0(q), q square-free. Let Δq denote the Laplace operator on L2(Γ\H), and let Σq denote its discrete spectrum. Then there exists an absolute positive constant A such that for q≧A

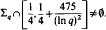
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 33 , Issue 2 , June 1990 , pp. 241 - 250
Copyright
Copyright © Edinburgh Mathematical Society 1990

References

REFERENCES

1.Buser, M., On Cheeger's inequality λ1≧h2/4, Proc. Sympos. Pure Math. 36 (1980), 29–77.CrossRefGoogle Scholar
2.Chavel, I., Lowest-eigenvalue inequalities, Proc. Sympos. Pure Math. 36, (1980), 79–89.CrossRefGoogle Scholar
3.Chavel, I., Eigenvalues in Riemannian Geometry (Academic Press, Inc., New York, 1984).Google Scholar
4.Gradshteyn, I. S. and Ryzhik, I. M., Tables of Integrals Series and Products (Academic Press, New York, 1980).Google Scholar
5.Hejhal, D., The Selberg Trace Formula for PSL (2, R) II (Lecture Notes in Math. 1001, Springer-Verlag, Berlin, New York, 1983).CrossRefGoogle Scholar
6.Huber, H., On the spectrum of the Laplace operator on compact Riemann surfaces, Proc. Sympos. Pure Math. 36 (1980), 181–184.CrossRefGoogle Scholar
7.Huxley, M. N., Conjugacy classes in congruence subgroups, preprint.Google Scholar
8.Huxley, M. N., Introduction to Kloostermania, in Elementary and Analytical Theory of Numbers (Banach Center Publ. 17, PWN, Warsaw, 1985), 217–306.Google Scholar
9.Huxley, M. N., Exceptional eigenvalues and congruence subgroups, Contemp. Math. 53 (1986), 341–349.CrossRefGoogle Scholar
10.Iwaniec, H., Small eigenvalues for congruence groups, preprint.Google Scholar
11.Iwaniec, H., Prime geodesic theorem, J. Reine Angew. Math. 349 (1984), 136–159.Google Scholar
12.Iwaniec, H., Character sums and small eigenvalues for Γ0(p), Glasgow Math. J. 27 (1985), 99–116.CrossRefGoogle Scholar
13.Iwaniec, H. and Szmidt, J., Density theorems for exceptional eigenvalues of Laplacian for congruence groups, Banach Center Publ. 17 (1984), 317–331.CrossRefGoogle Scholar
14.Randol, B., Small eigenvalues of the Laplace operator on compact Riemann surfaces, Bull. Amer. Math. Soc. 80 (1974), 996–1000.CrossRefGoogle Scholar
15.Reilly, R. C., Extrinsic estimates for λ1, Proc. Sympos. Pure Math 36 (1980), 275–278.CrossRefGoogle Scholar
16.Sarnak, P., Class numbers of indefinite binary quadratic forms, J. Number Theory 15 (1982), 229–247.CrossRefGoogle Scholar
17.Schoen, R., Wolpert, S. and Yau, S. T., Geometric bounds on the low eigenvalues of a compact surface, Proc. Sympos. Pure Math. 36 (1980), 279–285.CrossRefGoogle Scholar
18.Selberg, A., On the estimation of Fourier coefficients of modular forms, Proc. Sympos. Pure Math. 8 (1965), 1–15.CrossRefGoogle Scholar
19.Shimura, G., Introduction to the Arithmetic Theory of Automorphic Functions (Princeton University Press, 1971).Google Scholar
20.Sneddon, I. N., The Use of Integral Transforms (McGraw-Hill, New York, 1972).Google Scholar