Hostname: page-component-745bb68f8f-lrblm Total loading time: 0 Render date: 2025-01-14T22:59:39.490Z Has data issue: false hasContentIssue false
  • English
  • Français

An unpleasant set in a non-locally-convex vector lattice

Published online by Cambridge University Press:  20 January 2009

J. D. Pryce
J. D. Pryce
Affiliation:
University of Aberdeen
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In a linear topological space E one often carries out various “ smoothing ” operations on a subset A, such as taking the convex hull co A and the closure A-. If E is also a (real) vector lattice, the solid hull

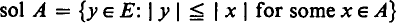
is also a natural “ smoothing out ” of A. If sol A = A then A is called solid, and if E has a base of solid neighbourhoods of 0 as do all the common topological vector lattices such as C(X), Lp, Köthe spaces and so on—then E is called a locally solid space.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 18 , Issue 3 , June 1973 , pp. 229 - 233
Copyright
Copyright © Edinburgh Mathematical Society 1973

References

REFERENCES

(1) Chacon, R. V. and Krengel, U., Linear modulus of a linear operator, Proc. Amer. Math. Soc. 15 (1964), 553–559.Google Scholar
(2) Peressini, A. L., Ordered Topological Vector Spaces (Harper, 1967).Google Scholar
(3) Breiman, L., Probability (Addison-Wesley, 1968).Google Scholar
(4) Feller, W., Introduction to Probability Theory and Applications, Vol. 2 (Wiley, 1966).Google Scholar
(5) Kingman, J. F. C. and Taylor, S. J., Introduction to Measure and Probability (Cambridge, 1966).Google Scholar
(6) Yosida, K., Functional Analysis, 2nd ed. (Springer, 1966).Google Scholar