Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-17T17:22:12.399Z Has data issue: false hasContentIssue false
  • English
  • Français

An iteration method for the determination of an unknown boundary condition in a parabolic initial-boundary value problem

Published online by Cambridge University Press:  20 January 2009

Michael Pilant  and
William Rundell
Michael Pilant
Affiliation:
Department of MathematicsTexas A & M UniversityCollege Station TX 77843USA
William Rundell
Affiliation:
Department of MathematicsTexas A & M UniversityCollege Station TX 77843USA
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Consider the initial boundary value problem

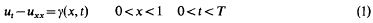
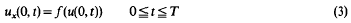
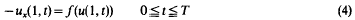
In the context of the heat conduction problem, this models the case where the heat flux across the ends at the rod is a function of the temperature. If the heat exchange between the rod and its surroundings is purely by convection, then one commonly assumes that f is a linear function of the difference in temperatures between the ends of the rod and that of the surroundings, (Newton's law of cooling). For the case of purely radiative transfer of energy a fourth power law for the function f is usual, (Stefan's law).

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 32 , Issue 1 , February 1989 , pp. 59 - 71
Copyright
Copyright © Edinburgh Mathematical Society 1989

References

REFERENCES

1Cannon, J. R., The one-dimensional heat equation, Encyclopedia Math. Appl. 23.Google Scholar
2Pilant, M. and Rundell, W., An inverse problem for a nonlinear parabolic equation, Comm. Partial Differential Equations 11 (4) (1986), 445–457.CrossRefGoogle Scholar
3Pilant, M. and Rundell, W., Undetermined coefficient problems for nonlinear elliptic and parabolic equations, Internat. Ser. Numer. Math. 77 (1986), 139–154.Google Scholar
4Pilant, M. and Rundell, W., An inverse problem for a nonlinear elliptic equation, SIAM J. Math. Anal., 18 (6) (1987), 1801–1809.CrossRefGoogle Scholar
5Pilant, M. and Rundell, W., Iteration schemes for unknown coefficient problems arising in parabolic equations, Numer. Methods in PDE, 3 (1987), 313–325.CrossRefGoogle Scholar