No CrossRef data available.
Published online by Cambridge University Press: 20 January 2009
The function
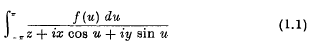
is, as is well-known, a general solution of Laplace's equation of degree −1 in (x, y, z). In 1926* I proved that the particular solution r−1Q0 (z/r) cannot be represented in this form whereas the solution r−1Q0 (y/r) can. In the present note I find a very simple expression for the latter solution in the form (1.1), and I deduce from it an apparently new integral formula for Qn (cos θ).
page 81 note * Proc. Edin. Math. Soc. (1), 44 (1926), 22–25. A slight correction is needed in that paper. I quoted an asymptotic formula for ![]() , due to Watson ; but as in that paper m is a positive integer, the expression given is the actual value of
, due to Watson ; but as in that paper m is a positive integer, the expression given is the actual value of ![]() without the order term.Google Scholar
without the order term.Google Scholar
page 82 note * Hobson, , Spherical and Ellipsoidal Harmonics (Cambridge, 1931), 70.Google Scholar