Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-26T00:55:41.101Z Has data issue: false hasContentIssue false
  • English
  • Français

An extension of the Forelli–Rudin projection theorem

Published online by Cambridge University Press:  20 January 2009

M. Mateljević  and
M. Pavlović
M. Mateljević
Affiliation:
Mathematički Fakultet, Studentski trg 16, 11000 Beograd, Yugoslavia
M. Pavlović
Affiliation:
Mathematički Fakultet, Studentski trg 16, 11000 Beograd, Yugoslavia
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For a measurable function f on the unit ball B in ℂn we define (M1f)(w), |w|<1, to be the mean modulus of f over a hyperbolic ball with center at w and of a fixed radius. The space 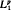, 0<p<∞, is defined by the requirement that M1f belongs to the Lebesgue space Lp. It is shown that the subspace of Lp spanned by holomorphic functions coincides with the corresponding subspace of 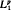. It is proved that if s>(n+1)(p−1−1), 0<p<1, then this subspace is complemented in 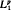by the projection whose reproducing kernel is 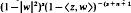. As corollaries we get an extension of the Forelli–Rudin projection theorem and we show that a holomorphic function f is Lp-integrable, 0<p<∞, over the unit ball B iff u = Ref is Lp-integrable over B. Finally, we sketch an alternative proof of the main result of this paper in the case 0<p<1.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 36 , Issue 3 , October 1993 , pp. 375 - 389
Copyright
Copyright © Edinburgh Mathematical Society 1993

References

REFERENCES

1.Axler, S., Bergman spaces and their operators, Surveys of some recent results on Operator Theory (Eds. Conway, John B. and Morrel, Bernard B., Pitman Research Notes in Mathematics, 1988).Google Scholar
2.Coifman, R. R. and Rochberg, R., Representation theorem for holomorphic and harmonic functions in Lp, Asterique 77 (1980), 11–66.Google Scholar
3.Fefferman, C. and Stein, E. M., Hp spaces of several variables, Acta Math. 129 (1972), 137–193.CrossRefGoogle Scholar
4.Forelli, F. and Rudin, W., Projections on spaces of holomorphic functions in balls, Indiana Univ. Math. J. 24 (1974), 593–602.CrossRefGoogle Scholar
5.Hardy, G. H. and Littlewood, J. E., Some properties of conjugate functions, J. Reine Angew. Math. 167 (1932), 405–423.Google Scholar
6.Mateuević, M., Bounded projections and decompositions in spaces of holomorphic functions, Mat. Vesnik 38 (1986), 521–528.Google Scholar
7.Leucking, D., Multipliers of Bergman spaces into Lebesgue spaces, Proc. Edinburgh Math. Soc. 29 (1986), 125–131.CrossRefGoogle Scholar
8.Pavlović, M., Mean values of harmonic conjugates in the unit disc, Complex Variables 10 (1988), 53–65.Google Scholar
9.Rochberg, R., Decomposition theorem for Bergman spaces and their applications, Operators and Function Theory (Ed. S. C. Power, 1985), 225–277.CrossRefGoogle Scholar
10.Rudin, W., Function Theory in the Unit Ball of Cn (Springer-Verlag, Berlin, Heidelberg, New York, 1980).CrossRefGoogle Scholar